Trong mặt phẳng \(Oxy\), cho các vectơ \(\vec{a}=(2;1)\), \(\vec{b}=(3;4)\) và \(\vec{c}=(7;2)\). Tìm giá trị của \(k,\,h\) sao cho $$\vec{c}=k\vec{a}+h\vec{b}$$

	\(\begin{cases}k=\dfrac{5}{2}\\ h=-\dfrac{13}{10}\end{cases}\)
	\(\begin{cases}k=\dfrac{23}{5}\\ h=-\dfrac{51}{10}\end{cases}\)
	\(\begin{cases}k=\dfrac{22}{5}\\ h=-\dfrac{3}{5}\end{cases}\)
	\(\begin{cases}k=\dfrac{17}{5}\\ h=-\dfrac{1}{5}\end{cases}\)

Trong mặt phẳng \(Oxy\), cho các vectơ \(\vec{a}=(m;2)\), \(\vec{b}=(-5;1)\) và \(\vec{c}=(m;7)\). Tìm giá trị của \(m\), biết rằng \(\vec{c}=2\vec{a}+3\vec{b}\).

	\(m=-15\)
	\(m=3\)
	\(m=15\)
	\(m=5\)

Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(P(4;5)\) và \(S(3;-1)\). Tìm tọa độ điểm \(H\) thỏa mãn $$\overrightarrow{OH}=2\overrightarrow{OP}-3\overrightarrow{OS}.$$

	\(H(-1;13)\)
	\(H(-1;7)\)
	\(H(-6;-17)\)
	\(H(1;-13)\)

Cho hình bình hành \(ABCD\) biết \(A(1;2)\), \(B(4;5)\) và \(D(3;-1)\). Tìm tọa độ điểm \(C\).

	\(C(2;8)\)
	\(C(6;2)\)
	\(C(0;-4)\)
	\(C\left(\dfrac{8}{3};2\right)\)

Tìm tọa độ trọng tâm \(G\) của tam giác \(ABC\) biết \(A(-1;3)\), \(B(1;-1)\) và \(C(3;7)\).

	\(G(3;9)\)
	\(G(1;3)\)
	\(G\left(\dfrac{3}{2};\dfrac{9}{2}\right)\)
	\(G(9;27)\)

Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) có \(A(-2;2)\), \(B(3;5)\) và trọng tâm là gốc tọa độ \(O\). Tìm tọa độ đỉnh \(C\).

	\(C(-1;-7)\)
	\(C(2;-2)\)
	\(C(-3;-5)\)
	\(C(1;7)\)

Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) có \(A(6;1)\), \(B(-3;5)\) và trọng tâm \(G(-1;1)\). Tìm tọa độ đỉnh \(C\).

	\(C(6;-3)\)
	\(C(-6;3)\)
	\(C(-6;-3)\)
	\(C(-3;6)\)

Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) có \(A(3;5)\), \(B(1;2)\), \(C(5;2)\). Tìm tọa độ trọng tâm \(G\) của tam giác.

	\(G(-3;-3)\)
	\(G\left(\dfrac{9}{2};\dfrac{9}{2}\right)\)
	\(G(9;9)\)
	\(G(3;3)\)

Trong mặt phẳng \(Oxy\), cho hai điểm \(A(2;-3)\), \(B(4;7)\). Tìm tọa độ trung điểm \(I\) của đoạn thẳng \(AB\).

	\(I(6;4)\)
	\(I(2;0)\)
	\(I(3;2)\)
	\(I(8;-21)\)

Trong mặt phẳng \(Oxy\), cho ba điểm \(A(1;3)\), \(B(-1;2)\) và \(C(-2;1)\). Tìm tọa độ vectơ \(\overrightarrow{AB}-\overrightarrow{AC}\).

	\(\overrightarrow{AB}-\overrightarrow{AC}=(-5;-3)\)
	\(\overrightarrow{AB}-\overrightarrow{AC}=(1;1)\)
	\(\overrightarrow{AB}-\overrightarrow{AC}=(-1;2)\)
	\(\overrightarrow{AB}-\overrightarrow{AC}=(-1;1)\)

Trong mặt phẳng \(Oxy\), cho hai điểm \(A(5;2)\) và \(B(10;8)\). Tìm tọa độ của vectơ \(\overrightarrow{AB}\).

	\(\overrightarrow{AB}=(15;10)\)
	\(\overrightarrow{AB}=(2;4)\)
	\(\overrightarrow{AB}=(5;6)\)
	\(\overrightarrow{AB}=(50;16)\)

Trong mặt phẳng tọa độ \(Oxy\), cho hai vectơ \(\vec{u}=(-1;2)\) và \(\vec{v}=(3;-2)\). Tính tọa độ của vectơ \(2\vec{u}-3\vec{v}\).

	\((11;-10)\)
	\((9;-10)\)
	\((-11;-2)\)
	\((-11;10)\)

Trong mặt phẳng \(Oxy\), tọa độ của vectơ \(\vec{i}+\vec{j}\) là

	\((0;1)\)
	\((1;-1)\)
	\((-1;1)\)
	\((1;1)\)

Trong mặt phẳng \(Oxy\), cho hai vectơ \(\vec{a}=(2;-4)\) và \(\vec{b}=(-5;3)\). Tìm tọa độ vectơ $\vec{u}=2\vec{a}-\vec{b}$.

	\(\vec{u}=(7;-7)\)
	\(\vec{u}=(9;-11)\)
	\(\vec{u}=(9;-5)\)
	\(\vec{u}=(-1;5)\)

Trong mặt phẳng \(Oxy\), cho hai vectơ \(\vec{a}=(-1;2)\) và \(\vec{b}=(5;-7)\). Tìm tọa độ vectơ $\vec{w}=\vec{a}-\vec{b}$.

	\(\vec{w}=(6;-9)\)
	\(\vec{w}=(4;-5)\)
	\(\vec{w}=(-6;9)\)
	\(\vec{w}=(-5;-14)\)

Trong mặt phẳng \(Oxy\), cho hai vectơ \(\vec{a}=(3;-4)\) và \(\vec{b}=(-1;2)\). Tìm tọa độ vectơ $\vec{v}=\vec{a}+\vec{b}$.

	\(\vec{v}=(-4;6)\)
	\(\vec{v}=(2;-2)\)
	\(\vec{v}=(4;-6)\)
	\(\vec{v}=(-3;-8)\)

Cho hàm số \(f(x)\) có bảng xét dấu của đạo hàm như sau:

Hàm số \(y=3f(x+2)-x^3+3x\) đồng biến trên khoảng nào sau đây:

	\((1;+\infty)\)
	\((-\infty;-1)\)
	\((-1;0)\)
	\((0;2)\)

Cho hàm số \(y=f(x)\) có đồ thị hàm số \(y=f'(x)\) như hình vẽ.

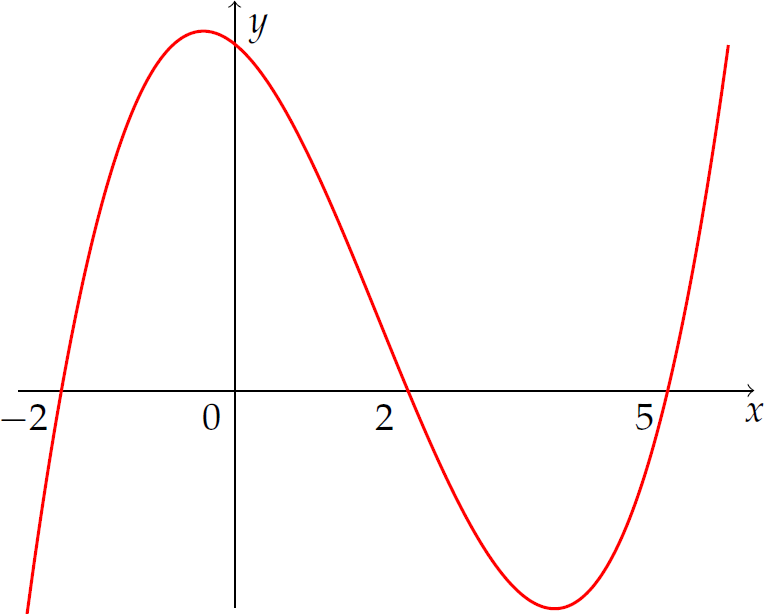
Hàm số \(y=f(3-2x)\) nghịch biến trên khoảng nào sau đây:

	\((-1;+\infty)\)
	\((0;2)\)
	\((-\infty;-1)\)
	\((1;3)\)

Cho hàm số \(y=f(x)\) thỏa mãn \(f'(x)=x^2-5x+4,\;\forall x\in\mathbb{R}\). Khẳng định nào sau đây là đúng?

	Hàm số đồng biến trên khoảng \((-\infty;3)\)
	Hàm số nghịch biến trên khoảng \((3;+\infty)\)
	Hàm số nghịch biến trên khoảng \((2;3)\)
	Hàm số đồng biến trên khoảng \((1;4)\)

Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x^2-2x,\;\forall x\in\mathbb{R}\). Hàm số \(y=-2f(x)\) đồng biến trên khoảng

	\((0;2)\)
	\((2;+\infty)\)
	\((-\infty;-2)\)
	\((-2;0)\)