Số phức liên hợp của số phức \(z=2+i\) là

	\(\overline{z}=-2+i\)
	\(\overline{z}=-2-i\)
	\(\overline{z}=2-i\)
	\(\overline{z}=2+i\)

Nếu \(\displaystyle\int\limits_0^1f\left(x\right)\mathrm{\,d}x=4\) thì \(\displaystyle\int\limits_0^12f\left(x\right)\mathrm{\,d}x\) bằng

	\(16\)
	\(4\)
	\(2\)
	\(8\)

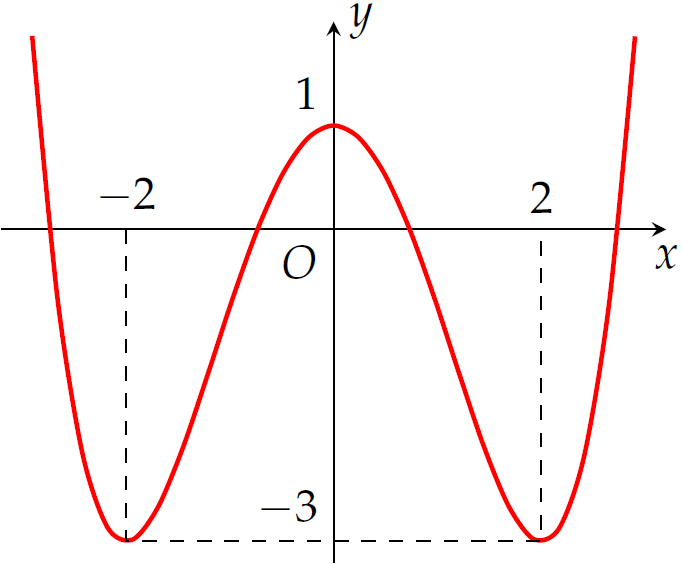
Cho hàm số \(y=f\left(x\right)\) có đồ thị trong hình vẽ trên. Số nghiệm của phương trình \(f\left(x\right)=-1\) là

	\(3\)
	\(2\)
	\(1\)
	\(4\)

Tập nghiệm của bất phương trình \(\log x\ge1\) là

	\(\left(10;+\infty\right)\)
	\(\left(0;+\infty\right)\)
	\(\left[10;+\infty\right)\)
	\(\left(-\infty;10\right)\)

Tiệm cận ngang của đồ thị hàm số \(y=\dfrac{x-2}{x+1}\) là

	\(y=-2\)
	\(y=1\)
	\(x=-1\)
	\(x=2\)

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình trên?

	\(y=x^3-3x\)
	\(y=-x^3+3x\)
	\(y=x^4-2x^2\)
	\(y=-x^4+2x\)

Cho hàm số \(y=f\left(x\right)\) có bảng biến thiên như sau:

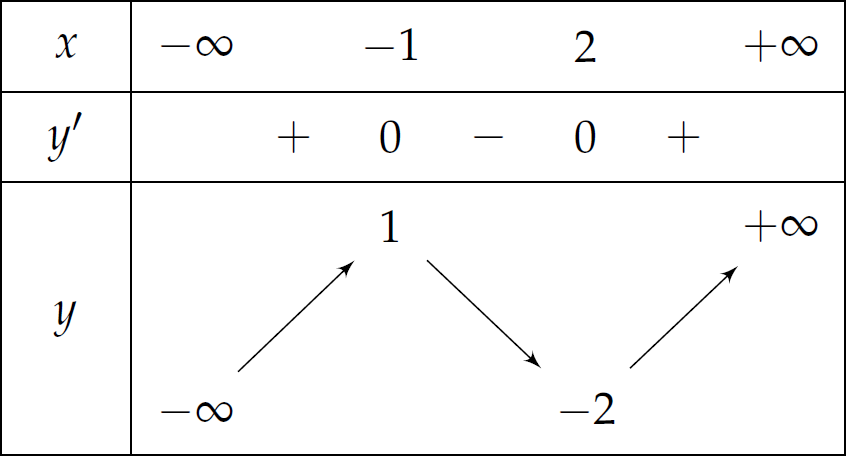
Hàm số đã cho đạt cực đại tại điểm

	\(x=-2\)
	\(x=2\)
	\(x=1\)
	\(x=-1\)

Diện tích xung quanh của hình trụ có độ dài đường sinh \(\ell\) và bán kính đáy \(r\) bằng

	\(4\pi r\ell\)
	\(\pi r\ell\)
	\(\dfrac{1}{3}\pi r\ell\)
	\(2\pi r\ell\)

Với \(a\) là số thực dương tùy ý, \(\log_2\left(a^3\right)\) bằng

	\(\left(\dfrac{3}{2}\log_2a\right)\)
	\(\dfrac{1}{3}\log_2a\)
	\(3+\log_2a\)
	\(3\log_2a\)

Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:

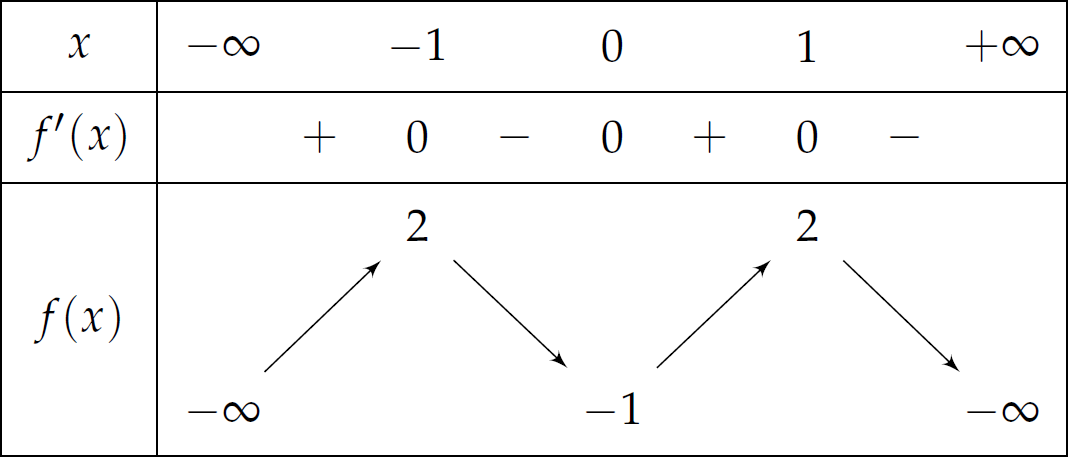
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

	\(\left(-\infty;-1\right)\)
	\(\left(0;1\right)\)
	\(\left(-1;0\right)\)
	\(\left(-\infty;0\right)\)

Cho mặt cầu có bán kính \(R=2\). Diện tích của mặt cầu đã cho bằng

	\(\dfrac{32\pi}{3}\)
	\(8\pi\)
	\(16\pi\)
	\(4\pi\)

Cho khối nón có chiều cao \(h=3\) và bán kính đáy \(r=4\). Thể tích của khối nón đã cho bằng

	\(16\pi\)
	\(48\pi\)
	\(36\pi\)
	\(4\pi\)

Cho khối chóp có diện tích đáy \(B=3\) và chiều cao \(h=4\). Thể tích của khối chóp đã cho bằng

	\(6\)
	\(12\)
	\(36\)
	\(4\)

Hàm số \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên khoảng \(K\) nếu

	\(F'(x)=-f(x),\,\forall x\in K\)
	\(f'(x)=F(x),\,\forall x\in K\)
	\(F'(x)=f(x),\,\forall x\in K\)
	\(f'(x)=-F(x),\,\forall x\in K\)

Tập xác định của hàm số \(y=\log_2x\) là

	\([0;+\infty)\)
	\((-\infty;+\infty)\)
	\((0;+\infty)\)
	\([2;+\infty)\)

Thể tích của khối lập phương cạnh \(2\) bằng

	\(6\)
	\(8\)
	\(4\)
	\(2\)

Nghiệm của phương trình \(3^{x-1}=27\) là

	\(x=4\)
	\(x=3\)
	\(x=2\)
	\(x=1\)

Cho cấp số cộng \(\left(u_n\right)\) với \(u_1=3\) và \(u_2=9\). Công sai của cấp số cộng đã cho bằng

	\(6\)
	\(3\)
	\(12\)
	\(-3\)

Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm \(10\) học sinh?

	\(\mathrm{C}_{10}^2\)
	\(\mathrm{A}_{10}^2\)
	\(10^2\)
	\(2^{10}\)

Trong không gian \(Oxyz\), cho mặt phẳng \((P)\colon x+y-z-1=0\) và điểm \(A(1;0;0)\in(P)\). Đường thẳng \(\Delta\) đi qua \(A\) nằm trong \((P)\) và tạo với trục \(Oz\) một góc nhỏ nhất. Gọi \(M\left(x_0;y_0;z_0\right)\) là giao điểm của đường thẳng \(\Delta\) với mặt phẳng \((Q)\colon2x+y-2z+1=0\). Tổng \(S=x_0+y_0+z_0\) bằng

	\(-2\)
	\(13\)
	\(-5\)
	\(12\)