Với \(a,\,b\) là hai số thực dương tùy ý, \(\log\left(a^2b^3\right)\) bằng

	\(2\log a\cdot3\log b\)
	\(\dfrac{1}{2}\log a+\dfrac{1}{3}\log b\)
	\(2\log a+3\log b\)
	\(2\log a+\log b\)

Hàm số nào sau đây không có điểm cực trị?

	\(y=-x^4+2x^2-5\)
	\(y=x^4+2x^2-5\)
	\(y=-\dfrac{1}{4}x^4+6\)
	\(y=x^3+6x-2019\)

Nếu hàm số \(y=f(x)\) thỏa mãn \(\lim\limits_{x\to1^-}f(x)=-\infty\) thì đồ thị hàm số \(y=f(x)\) có đường tiệm cận đứng là đường thẳng có phương trình

	\(x=-1\)
	\(x=1\)
	\(y=1\)
	\(y=-1\)

Cho \(x,\,y\) là hai số thực dương và \(m,\,n\) là hai số thực tùy ý. Đẳng thức nào sau đây là sai?

	\(\left(x^m\right)^n=x^{mn}\)
	\(x^m\cdot x^n=x^{m+n}\)
	\((xy)^n=x^ny^n\)
	\(x^my^n=(xy)^{m+n}\)

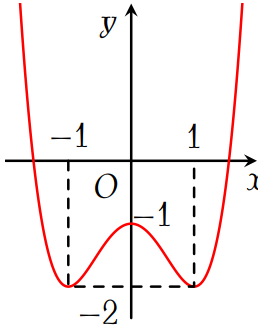
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ. Giá trị cực đại của hàm số bằng

	\(1\)
	\(-2\)
	\(-1\)
	\(0\)

Cho \(\alpha\) là một số thực dương. Viết \(\alpha^{\tfrac{2}{3}}\cdot\sqrt{\alpha}\) dưới dạng lũy thừa với số mũ hữu tỷ.

	\(\alpha^{\tfrac{7}{6}}\)
	\(\alpha^{\tfrac{5}{3}}\)
	\(\alpha^{\tfrac{1}{3}}\)
	\(\alpha^{\tfrac{7}{3}}\)

Tính \(P=\left(\dfrac{1}{16}\right)^{-0,75}+(0,25)^{-\tfrac{5}{2}}\).

	\(P=80\)
	\(P=40\)
	\(P=10\)
	\(P=20\)

Tập xác định \(\mathscr{D}\) của hàm số \(y=(x+1)^{\tfrac{1}{3}}\) là

	\(\mathscr{D}=\mathbb{R}\setminus\{-1\}\)
	\(\mathscr{D}=(-1;+\infty)\)
	\(\mathscr{D}=\mathbb{R}\)
	\(\mathscr{D}=(-\infty;-1)\)

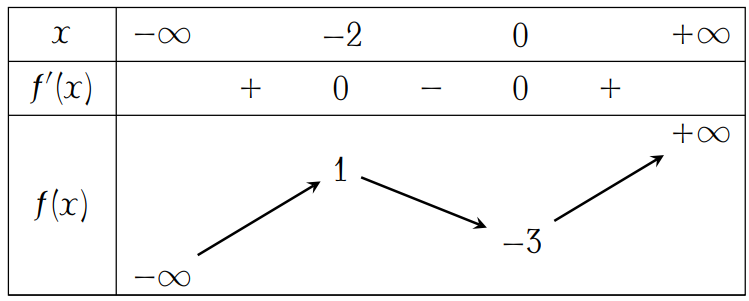
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Hàm số nghịch biến trên khoảng nào dưới đây?

	\((-\infty;-2)\)
	\((0;+\infty)\)
	\((1;-3)\)
	\((-2;0)\)

Cho hình chóp \(S.ABCD\) đáy là hình chữ nhật \(AD=2a\), \(AB=a\) (\(a>0\)), có \(\left(SAB\right)\) và \(\left(SAD\right)\) vuông góc đáy và góc \(SC\) và đáy bằng \(30^\circ\). Thể tích khối chóp là

	\(\dfrac{2a^3}{3}\)
	\(\dfrac{2a^3\sqrt{15}}{9}\)
	\(\dfrac{a^3\sqrt{3}}{3}\)
	\(\dfrac{a^3\sqrt{3}}{6}\)

Đa diện đều loại {5,3} có tên gọi nào dưới đây:

	Hai mươi mặt đều
	Lập phương
	Tứ diện đều
	Mười hai mặt đều

Trong một phép thử ngẫu nhiên, nếu hai biến cố \(A\) và \(B\) độc lập thì mệnh đề nào sau đây là đúng?

	\(P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)\)
	\(P\left(A\cap B\right)=P\left(A\right)+P\left(B\right)\)
	\(P\left(A\cup B\right)=P\left(A\right)\cdot P\left(B\right)\)
	\(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)\)

Cho \(A\) là một biến cố liên quan đến phép thử \(T\). Mệnh đề nào sau đây là đúng?

	\(P(A)<1\)
	\(P(A)>0\)
	\(P(A)=1-P\left(\overline{A}\right)\)
	\(0< P(A)<1\)

Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Xét biến cố \(A\colon\)"Kết quả gieo có số chấm không vượt quá \(4\)". Chọn mệnh đề đúng trong các mệnh đề dưới đây:

	\(A=\{1;2;3;4\}\)
	\(A=\{5;6\}\)
	\(A=\{1;2;3\}\)
	\(A=\{4;5;6\}\)

Gieo một con súc sắc cân đối và đồng chất hai lần. Tính số phần tử của biến cố "Tổng số chấm của hai lần gieo không quá \(5\)".

	\(10\)
	\(8\)
	\(11\)
	\(9\)

Gieo ngẫu nhiên một con súc sắc hai lần. Xét biến cố \(A\colon\)"Lần thứ hai xuất hiện mặt ba chấm". Chọn phương án đúng.

	\(A=\left\{(3;1),(3;2),(3;3),(3;4),(3;5),(3;6)\right\}\)
	\(A=\left\{(3;1),(3;2),(3;4),(3;5),(3;6)\right\}\)
	\(A=\left\{(1;3),(2;3),(3;3),(4;3),(5;3),(6;3)\right\}\)
	\(A=\left\{(3;3)\right\}\)

Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất \(3\) lần. Khi đó \(n\left(\Omega\right)\) bằng

	\(216\)
	\(36\)
	\(18\)
	\(120\)

Cho \(A\) và \(B\) là hai biến cố đối nhau. Khẳng định nào sau đây sai?

	\(A=\Omega\setminus B\)
	\(A\setminus B=\varnothing\)
	\(A\cup B=\Omega\)
	\(A\cap B=\varnothing\)

Gọi \(A\) và \(B\) là hai biến cố của một phép thử. Khẳng định nào sau đây là sai?

	Nếu \(A\cap B=\varnothing\) thì \(A\) và \(B\) đối nhau
	Nếu \(P(B)=0\) thì \(B\) là biến cố không thể
	Nếu \(P(A)=1\) thì \(A\) là biến cố chắc chắn
	Nếu \(A\) và \(B\) đối nhau thì \(P(A)+P(B)=1\)

Hai người độc lập ném bóng vào rổ của mình. Gọi \(A\) là biến cố "Cả hai người đều ném không trúng vào rổ", \(B\) là biến cố "Có ít nhất một người ném trúng vào rổ". Khẳng định nào sau đây là đúng?

	\(A\) và \(B\) là hai biến cố chắc chắn
	\(A\) và \(B\) là hai biến cố không thể
	\(A\) và \(B\) là hai biến cố đối nhau
	\(A\) và \(B\) là hai biến cố xung khắc nhưng không đối nhau