Một vật nhỏ dao động điều hòa dọc theo trục $Ox$ với tần số góc $\omega$ và có biên độ $A$. Biết gốc tọa độ $O$ ở vị trí cân bằng của vật. Chọn gốc thời gian là lúc vật ở vị trí có li độ $\dfrac{A}{2}$ và đang chuyển động theo chiều dương. Phương trình dao động của vật là
| $x=A\cos\left(\omega t-\dfrac{\pi}{3}\right)$ | |
| $x=A\cos\left(\omega t-\dfrac{\pi}{4}\right)$ | |
| $x=A\cos\left(\omega t+\dfrac{\pi}{3}\right)$ | |
| $x=A\cos\left(\omega t+\dfrac{\pi}{4}\right)$ |
Mối liên hệ về pha giữa các đại lượng li độ $\overrightarrow{x}$, vận tốc $\overrightarrow{v}$, gia tốc $\overrightarrow{a}$ trong dao động điều hòa được mô tả bằng hình nào?
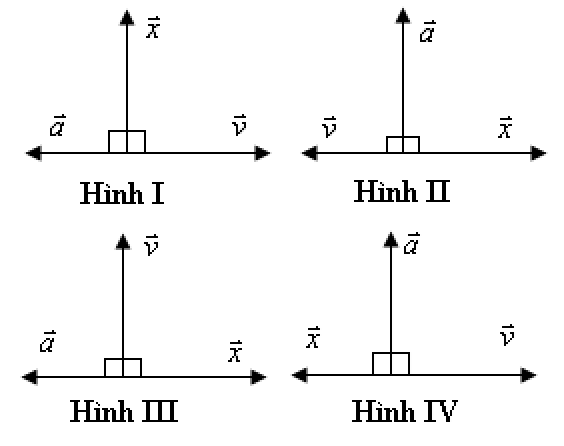
| Hình III | |
| Hình II | |
| Hình I | |
| Hình IV |
Một vật dao động điều hòa, có quãng đường đi được trong một chu kì là $16$cm. Biên độ dao động của vật là
| $4$cm | |
| $8$cm | |
| $16$cm | |
| $2$cm |
Một vật dao động điều hòa, có quỹ đạo là một đoạn thẳng dài $10$cm. Biên độ dao động của vật là
| $5$cm | |
| $10$cm | |
| $2,5$cm | |
| $7,5$cm |
Một vật nhỏ dao động theo phương trình $x=5\cos(\omega t+0,5\pi)$cm. Pha ban đầu của dao động là
| $0,5\pi$ | |
| $\pi$ | |
| $0,25\pi$ | |
| $1,5\pi$ |
Một vật dao động điều hòa theo phương trình $x=6\cos(4\pi t)$cm, biên độ dao động của vật là
| $6$cm | |
| $4$cm | |
| $4$m | |
| $6$m |
Trong dao động điều hòa, vận tốc của vật
| tăng khi vật về vị trí cân bằng | |
| giảm khi vật về vị trí cân bằng | |
| tăng khi vật ra xa vị trí cân bằng | |
| không đổi |
Nói về một chất điểm dao động điều hòa, phát biểu nào dưới đây đúng?
| Ở vị trí cân bằng, chất điểm có độ lớn vận tốc cực đại và gia tốc bằng không | |
| Ở vị trí cân bằng, chất điểm có vận tốc bằng không và gia tốc cực đại | |
| Ở vị trí biên, chất điểm có vận tốc bằng không và gia tốc bằng không | |
| Ở vị trí biên, chất điểm có độ lớn vận tốc cực đại và gia tốc cực đại |
Gia tốc của một chất điểm dao động điều hòa biến thiên
| cùng tần số, ngược pha với li độ | |
| khác tần số, cùng pha với li độ | |
| khác tần số, ngược pha với li độ | |
| cùng tần số, cùng pha với li độ |
Một vật nhỏ dao động điều hòa trên trục $Ox$. Trong các đại lượng sau của vật: biên độ, vận tốc, gia tốc, động năng thì đại lượng không thay đổi theo thời gian là
| biên độ | |
| động năng | |
| gia tốc | |
| vận tốc |
Vectơ vận tốc của một vật dao động điều hòa luôn
| hướng về vị trí cân bằng | |
| cùng hướng chuyển động. | |
| hướng ra xa vị trí cân bằng | |
| ngược hướng chuyển động. |
Trong dao động điều hòa, phát biểu nào sau đây là không đúng?
| Cứ sau một khoảng thời gian một chu kì thì li độ của vật lại không trở về giá trị ban đầu | |
| Cứ sau một khoảng thời gian một chu kì thì vận tốc của vật lại trở về giá trị ban đầu | |
| Cứ sau một khoảng thời gian một chu kì thì gia tốc của vật lại trở về giá trị ban đầu | |
| Cứ sau một khoảng thời gian một chu kì thì vật lại trở về vị trí ban đầu |
Vận tốc của chất điểm dao động điều hòa có độ lớn cực đại khi
| li độ bằng không | |
| li độ có độ lớn cực đại | |
| pha cực đại | |
| gia tốc có độ lớn cực đại |
C
Trong dao động điều hòa, li độ, vận tốc và gia tốc là ba đại lượng biến đổi điều hòa theo thời gian và có
| cùng tần số góc | |
| cùng pha | |
| cùng biên độ | |
| cùng pha ban đầu |
Khi nói về dao động điều hòa của một vật, phát biểu nào sau đây sai?
| Vectơ vận tốc và vectơ gia tốc của vật luôn ngược chiều nhau | |
| Lực kéo về luôn hướng về vị trí cân bằng | |
| Chuyển động của vật từ vị trí cân bằng ra vị trí biên là chuyển động chậm dần | |
| Vectơ gia tốc của vật luôn hướng về vị trí cân bằng và có độ lớn tỉ lệ với độ lớn của li độ |
Trong dao động điều hòa thì
| Vận tốc biến thiên điều hòa | |
| Lực phục hồi là lực đàn hồi | |
| Quỹ đạo là một đoạn thẳng | |
| gia tốc tỉ lệ thuận với thời gian |
Khi một vật dao động điều hòa, chuyển động của vật từ vị trí cân bằng ra vị trí biên dương là chuyển động
| chậm dần | |
| nhanh dần | |
| chậm dần đều | |
| nhanh dần đều |
Đối với dao động điều hòa, pha của dao động được dùng để xác định
| trạng thái dao động | |
| biên độ dao động | |
| chu kỳ dao động | |
| tần số dao động |
Đối với dao động điều hòa, khoảng thời gian ngắn nhất sau đó trạng thái dao động lặp lại như cũ gọi là
| chu kỳ dao động | |
| pha ban đầu | |
| tần số góc | |
| tần số dao động |
Một vật dao động điều hòa trên trục $Ox$ quanh vị trí cân bằng $O$. Vectơ gia tốc của vật
| có độ lớn tỉ lệ thuận với độ lớn li độ của vật | |
| có độ lớn tỉ lệ nghịch với tốc độ của vật | |
| luôn hướng ngược chiều chuyển động của vật | |
| luôn hướng theo chiều chuyển động của vật |
