Phát biểu nào sau đây đúng?
| Hàm số $y=f(x)$ đạt cực trị tại $x_0$ khi và chỉ khi $x_0$ là nghiệm của đạo hàm | |
| Nếu $f'\big(x_0\big)=0$ và $f''\big(x_0\big)>0$ thì hàm số đạt cực đại tại $x_0$ | |
| Nếu $f'\big(x_0\big)=0$ và $f''\big(x_0\big)=0$ thì $x_0$ không phải là cực trị của hàm số $y=f(x)$ đã cho | |
| Nếu $f'(x)$ đổi dấu khi $x$ qua điểm $x_0$ và $y=f(x)$ liên tục tại $x_0$ thì hàm số $y=f(x)$ đạt cực trị tại điểm $x_0$ |
Rút gọn biểu thức $A=\dfrac{\sqrt[3]{a^7}\cdot a^{\tfrac{11}{3}}}{a^4\cdot\sqrt[7]{a^{-5}}}$ với $a>0$ ta được kết quả là
| $A=a^{\tfrac{9}{7}}$ | |
| $A=a^{\tfrac{19}{7}}$ | |
| $A=a^{\tfrac{43}{5}}$ | |
| $A=a^{\tfrac{157}{105}}$ |
Cho ba số thực dương $A,\,B,\,C$ khác $1$ thỏa $B^2=AC$. Mệnh đề nào sau đây đúng?
| $\ln A+\ln C=2\ln B$ | |
| $\ln A\cdot\ln C=2\ln B$ | |
| $\ln A\cdot\ln C=\big(\ln B\big)^2$ | |
| $\ln A+\ln C=\ln B$ |
Cho hàm số $y=f(x)$ có bảng biến thiên sau:
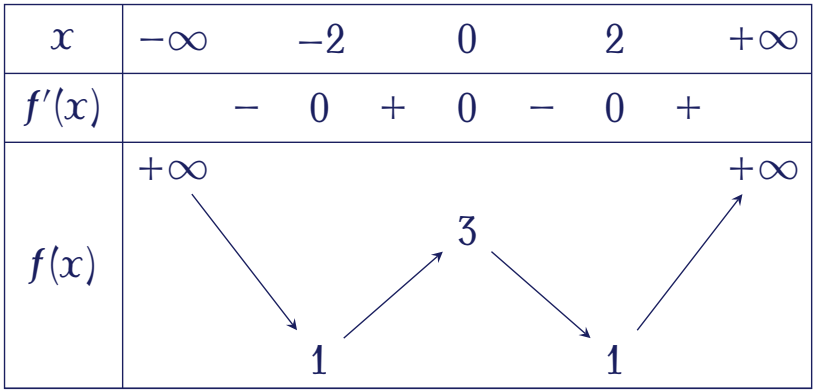
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
| $(1;3)$ | |
| $(-\infty;-2)$ | |
| $(0;+\infty)$ | |
| $(-2;0)$ |
Trong các hình dưới đây, hình nào là hình đa diện?
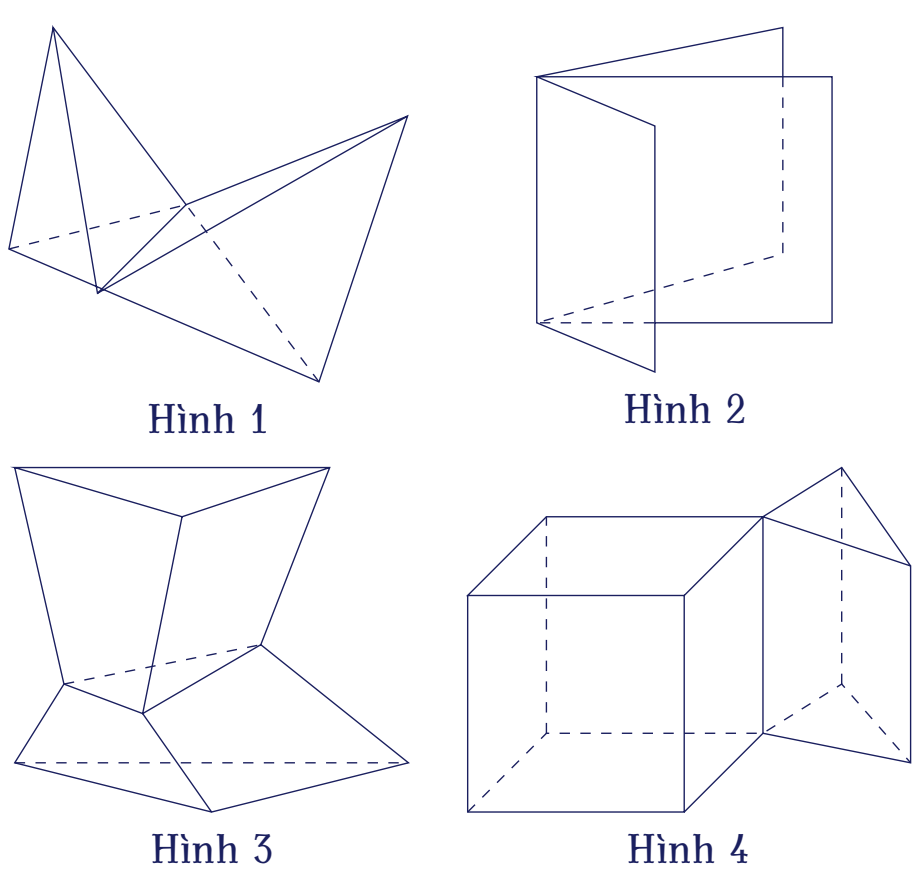
| Hình 4 | |
| Hình 2 | |
| Hình 1 | |
| Hình 3 |
Cho đồ thị các hàm số $y=x^\alpha$ và $y=x^\beta$ trên khoảng $(0;+\infty)$.
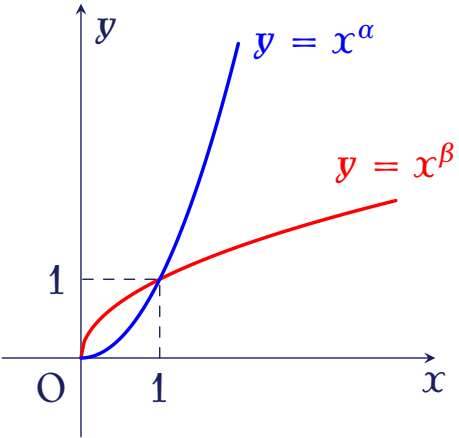
Mệnh đề nào dưới đây đúng?
| $0< \alpha< 1< \beta$ | |
| $\alpha< 0< 1< \beta$ | |
| $0< \beta< 1< \alpha$ | |
| $\beta< 0< 1< \alpha$ |
Với mọi số nguyên dương $n$, để chứng minh $3^{2n+1}+2^{n+2}$ chia hết cho $7$ bằng phương pháp quy nạp toán học, sau giả thiết quy nạp ta cần chứng minh điều gì?
| $3^{2n+1}+2^{n+2}$ chia hết cho $8$ | |
| $3^{2k+1}+2^{k+2}$ chia hết cho $7$ | |
| $3^{2k+1}+2^{k+2}$ chia hết cho $8$ | |
| $3^{2k+3}+2^{k+3}$ chia hết cho $7$ |
Với mọi số nguyên dương $n$, để chứng minh $7\cdot2^{2n-2}+3^{2n-1}$ chia hết cho $5$ bằng phương pháp quy nạp toán học, sau giả thiết quy nạp ta cần chứng minh điều gì?
| $7\cdot2^{2n-2}+3^{2n-1}$ chia hết cho $6$ | |
| $7\cdot2^{2k-2}+3^{2k-1}$ chia hết cho $5$ | |
| $7\cdot2^{2k}+3^{2k+1}$ chia hết cho $6$ | |
| $7\cdot2^{2k}+3^{2k+1}$ chia hết cho $5$ |
Với mọi số nguyên dương $n$, tổng $S_n=3^{2n+1}+2^{n+2}$ chia hết cho
| $7$ | |
| $35$ | |
| $5$ | |
| $259$ |
Với mọi số nguyên dương $n$, tổng $S_n=7\cdot2^{2n-2}+3^{2n-1}$ chia hết cho
| $2$ | |
| $3$ | |
| $5$ | |
| $10$ |
Với $\forall n\in\mathbb{N}^*$, biểu thức $13^n-1$ luôn chia hết cho
| $13$ | |
| $12$ | |
| $36$ | |
| $168$ |
Với $\forall n\in\mathbb{N}^*$, để chứng minh $13^n-1$ chia hết cho $6$ bằng phương pháp quy nạp toán học, sau giả thiết quy nạp ta cần chứng minh điều gì?
| $13^n-1$ chia hết cho $6$ | |
| $13^k-1$ chia hết cho $6$ | |
| $13^{k+1}-1$ chia hết cho $6$ | |
| $13^k+1$ chia hết cho $6$ |
Với $\forall n\in\mathbb{N}^*$, để chứng minh $13^n-1$ chia hết cho $6$ bằng phương pháp quy nạp toán học, giả thiết quy nạp là
| $13^n-1$ chia hết cho $6$ | |
| $13^k-1$ chia hết cho $6$ | |
| $13^{k+1}-1$ chia hết cho $6$ | |
| $13^k+1$ chia hết cho $6$ |
Với mọi số nguyên dương $n$, để chứng minh $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2n-1)(2n+1)}=\dfrac{n}{2n+1}$ bằng phương pháp quy nạp toán học, sau giả thiết quy nạp ta cần chứng minh điều gì?
| $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2k-1)(2k+1)}+\dfrac{1}{(2k+1)(2k+3)}=\dfrac{k+1}{2k+3}$ | |
| $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2k-1)(2k+1)}=\dfrac{k+1}{2k+3}$ | |
| $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2k-1)(2k+1)}=\dfrac{k}{2k+1}$ | |
| $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2k-1)(2k+1)}+\dfrac{1}{(2k+1)(2k+3)}=\dfrac{k}{2k+1}$ |
Với mọi số nguyên dương $n$, đặt $S_n=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2n-1)(2n+1)}$. Để chứng minh $S_n=\dfrac{n}{2n+1}$ bằng phương pháp quy nạp toán học, sau giả thiết quy nạp ta cần chứng minh điều gì?
| $S_{k+1}=\dfrac{k+1}{2k+3}$ | |
| $S_{k+1}=\dfrac{k}{2k+1}$ | |
| $S_k=\dfrac{k}{2k+1}$ | |
| $S_{k+1}=\dfrac{k+1}{2k+1}$ |
Với mọi số nguyên dương $n$, tổng $S_n=n^3+3n^2+5n+3$ luôn chia hết cho
| $3$ | |
| $4$ | |
| $5$ | |
| $7$ |
Với mỗi số nguyên dương $n$, kí hiệu $u_n=5\cdot2^{3n-2}+3^{3n-1}$. Một học sinh chứng minh $u_n$ luôn chia hết cho $19$ như sau:
- Bước 1. Khi $n=1$, ta có $u_1=5\cdot2^1+3^2=19$ chia hết cho $19$.
- Bước 2. Giả sử $u_k=5\cdot2^{3k-2}+3^{3k-1}$ chia hết cho $19$, với $k\geq1$.
Khi đó $\begin{aligned}[t] u_{k+1}&=5\cdot2^{3k+1}+3^{3k+2}\\ &=2^3\cdot5\cdot2^{3k-2}+3^3\cdot3^{3k-1}\\ &=8\cdot5\cdot2^{3k-2}+8\cdot3^{3k-1}+19\cdot3^{3k-1}\\ &=8\big(5\cdot2^{3k-2}+3^{3k-1}\big)+19\cdot3^{3k-1}. \end{aligned}$ - Bước 3. Vì $5\cdot2^{3k-2}+3^{3k-1}$ và $19\cdot3^{3k-1}$ chia hết cho $19$ nên $u_{k+1}$ chia hết cho $19$
Vậy $u_n$ chia hết cho $19$ với $\forall n\in\mathbb{N}$.
Lập luận trên đúng hay sai? Nếu sai thì sai từ bước nào?
| Sai từ bước 1 | |
| Sai từ bước 2 | |
| Sai ở bước 3 | |
| Đúng |
Với số tự nhiên $n$, mệnh đề nào sau đây là đúng?
| $2^n>2n+1,\,\forall n\geq2$ | |
| $2^n>2n+1,\,\forall n\geq3$ | |
| $2^n>2n+1,\,\forall n\geq1$ | |
| $2^n>2n+1,\,\forall n\in\mathbb{N}$ |
Bất đẳng thức $2^n>2n+1$ đúng với những số tự nhiên nào sau đây?
| $n\geq3$ | |
| $n\leq3$ | |
| $n\geq0$ | |
| $n\geq1$ |
Để chứng minh mệnh đề "$2^n>2n+1$ với mọi số tự nhiên $n\geq3$" bằng phương pháp quy nạp toán học, giả thiết quy nạp là
| $2^{k+1}>2{k+1}+1$, với $k\geq3$ | |
| $2^k>2k+1$, với $k=3$ | |
| $2^k>2k+1$, với $k\geq3$ | |
| $2^k>2k+1$, với $k\geq1$ |
