Cho khối lăng trụ $ABC.A'B'C'$ có thể tích bằng $V$. Thể tích của khối đa diện $ABCC'B'$ bằng
| $\dfrac{3V}{4}$ | |
| $\dfrac{2V}{3}$ | |
| $\dfrac{V}{2}$ | |
| $\dfrac{V}{4}$ |
Cho khối chóp $S.ABCD$ có đáy là hình bình hành và có thể tích $48$. Trên các cạnh $SA,\,SB,\,SC,\,SD$ lần lượt lấy các điểm $A',\,B',\,C'$ và $D'$ sao cho $\dfrac{SA'}{SA}=\dfrac{SC'}{SC}=\dfrac{1}{3}$ và $\dfrac{SB'}{SB}=\dfrac{SD'}{SD}=\dfrac{3}{4}$. Tính thể tích $V$ của khối đa diện lõm $S.A'B'C'D'$.
| $V=4$ | |
| $V=9$ | |
| $V=\dfrac{3}{2}$ | |
| $V=6$ |
Cho tứ diện $ABCD$. Các điểm $M$, $N$, $P$ lần lượt thuộc các cạnh $AB$, $AC$, $AD$ sao cho $MA=MB$, $NA=2NC$, $PA=3PD$. Biết thể tích khối tứ diện $AMNP$ bằng $V$ thì khối tứ diện $ABCD$ tính theo $V$ có giá trị là
| $4V$ | |
| $6V$ | |
| $12V$ | |
| $8V$ |
Cho hình chóp $S.ABC$, gọi $M$, $N$ lần lượt là trung điểm của cạnh $SA$, $SB$. Tính tỉ số $\dfrac{\mathrm{V}_{S.ABC}}{\mathrm{V}_{S.MNC}}$.
| $4$ | |
| $\dfrac{1}{2}$ | |
| $2$ | |
| $\dfrac{1}{4}$ |
Cho tứ diện $MNPQ$. Gọi $I,\,J,\,K$ lần lượt là trung điểm của các cạnh $MN,\,MP,\,MQ$.
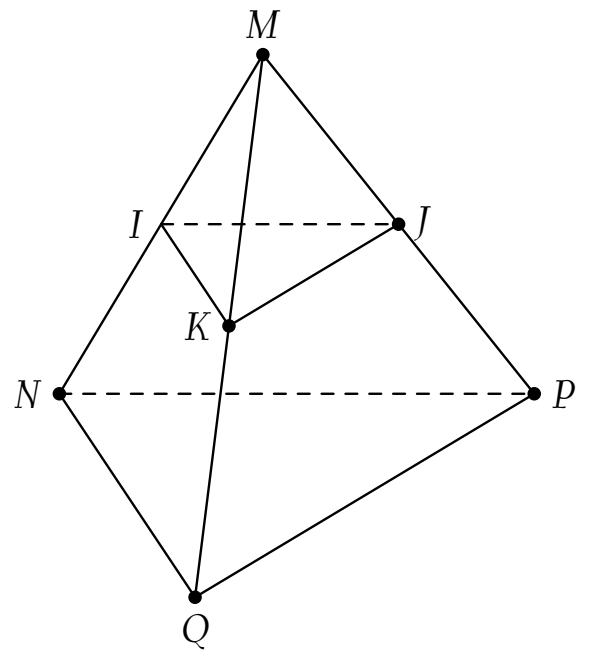
Tỉ số $\dfrac{V_{MIJK}}{V_{MNPQ}}$ bằng
| $\dfrac{1}{3}$ | |
| $\dfrac{1}{4}$ | |
| $\dfrac{1}{8}$ | |
| $\dfrac{1}{6}$ |
Cho hình chóp tam giác $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a$ và $SA$ vuông góc với mặt phẳng $(ABC)$ (tham khảo hình vẽ).
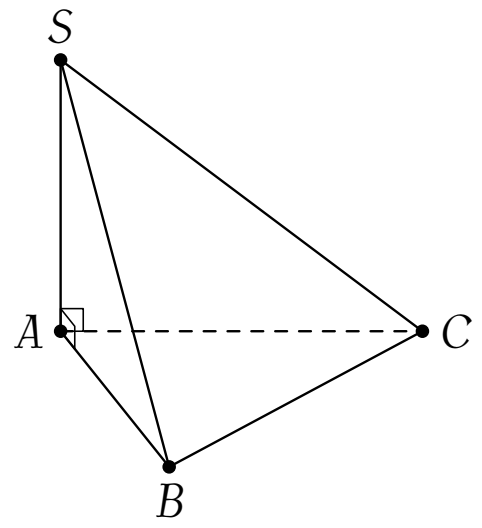
Biết thể tích của khối chóp $S.ABC$ là $\dfrac{a^3\sqrt{3}}{2}$ và góc giữa hai mặt phẳng $(SBC)$ và $(ABC)$ là góc nhọn $\alpha$. Chọn phát biểu đúng.
| $\alpha=60^{\circ}$ | |
| $\alpha=45^{\circ}$ | |
| $\alpha=30^{\circ}$ | |
| $\tan\alpha=\dfrac{\sqrt{3}}{2}$ |
Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng nhau và thể tích của khối lăng trụ bằng $2\sqrt{3}$. Tính cạnh của khối lăng trụ.
| $6$ | |
| $4$ | |
| $3$ | |
| $2$ |
Cho hình chóp đều $S.ABCD$ có chiều cao bằng $a\sqrt{2}$ và độ dài cạnh bên bằng $a\sqrt{6}$. Tính thể tích khối chóp $S.ABCD$.
| $\dfrac{8a^3\sqrt{2}}{3}$ | |
| $\dfrac{10a^3\sqrt{2}}{3}$ | |
| $\dfrac{8a^3\sqrt{3}}{3}$ | |
| $\dfrac{10a^3\sqrt{3}}{3}$ |
Cho khối chóp tứ giác đều có tất cả các cạnh bằng $2a$. Thể tích của khối chóp đã cho bằng
| $\dfrac{4\sqrt{2}a^3}{3}$ | |
| $\dfrac{8a^3}{3}$ | |
| $\dfrac{8\sqrt{2}a^3}{3}$ | |
| $\dfrac{2\sqrt{2}a^3}{3}$ |
Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh bằng $2a$. Hình chiếu vuông góc của $A'$ lên mặt phẳng $(ABC)$ trùng với trung điểm $H$ của cạnh $BC$ và $A'H=a\sqrt{3}$. Tính theo $a$ thể tích $V$ của khối lăng trụ $ABC.A'B'C'$.
| $V=3a^3$ | |
| $V=a^3$ | |
| $V=\dfrac{3a^3}{4}$ | |
| $V=\dfrac{3a^3}{2}$ |
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên hợp với mặt đáy một góc $60^\circ$. Tính theo $a$ thể tích $V$ của khối chóp $S.ABCD$.
| $V=\dfrac{a^3\sqrt{6}}{6}$ | |
| $V=\dfrac{a^3\sqrt{6}}{2}$ | |
| $V=\dfrac{a^3\sqrt{6}}{3}$ | |
| $V=\dfrac{a^3}{3}$ |
Tính thể tích khối rubic lập phương có cạnh bằng $8$cm (Bỏ các khe hở của khối rubic, xem thể tích của khe hở không đáng kể).
| $24\,\mathrm{cm}^3$ | |
| $8\,\mathrm{cm}^3$ | |
| $512\,\mathrm{cm}^3$ | |
| $\dfrac{512}{3}\,\mathrm{cm}^3$ |
Một viên gạch dạng khối hộp chữ nhật có ba kích thước là $3$cm, $10$cm, $20$cm. Tính thể tích viên gạch đó.
| $300$cm$^3$ | |
| $200$cm$^3$ | |
| $600$cm$^3$ | |
| $1200$cm$^3$ |
Nếu ba kích thước của một khối hộp chữ nhật tăng lên $3$ lần thì thể tích của nó tăng lên bao nhiêu lần?
| $3$ lần | |
| $9$ lần | |
| $18$ lần | |
| $27$ lần |
Cho khối lăng trụ có diện tích đáy là $30a^2$ và thể tích là $150a^3$. Tính theo $a$ khoảng cách giữa hai mặt phẳng đáy của khối lăng trụ đã cho.
| $h=5$ | |
| $h=5a$ | |
| $h=\dfrac{a}{5}$ | |
| $h=15a$ |
Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a\sqrt{3}$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Biết rằng thể tích của khối chóp $S.ABC$ bằng $\sqrt{3}a^3$. Tính độ dài cạnh $SA$.
| $2a\sqrt{3}$ | |
| $\sqrt{3}$ | |
| $2a$ | |
| $a$ |
Cho khối chóp $S.ABC$ có đáy là tam giác đều cạnh $2a$ và thể tích bằng $a^3$. Tính chiều cao $h$ của hình chóp đã cho.
| $h=\dfrac{\sqrt{3}a}{6}$ | |
| $h=\dfrac{\sqrt{3}a}{2}$ | |
| $h=\dfrac{\sqrt{3}a}{3}$ | |
| $h=\sqrt{3}a$ |
Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác đều, $SA$ vuông góc với mặt phẳng $(ABC)$ và $SA=a$. Biết rằng thể tích của khối chóp $S.ABC$ bằng $\sqrt{3}a^3$. Tính độ dài cạnh đáy của khối chóp $S.ABC$.
| $2a\sqrt{3}$ | |
| $3a\sqrt{3}$ | |
| $2a$ | |
| $2a\sqrt{2}$ |
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA\perp(ABCD)$ và $SA=a\sqrt{6}$. Thể tích của khối chóp $S.ABCD$ bằng
| $a^3\sqrt{6}$ | |
| $a^3\dfrac{\sqrt{6}}{3}$ | |
| $a^3\dfrac{\sqrt{6}}{6}$ | |
| $a^3\dfrac{\sqrt{6}}{2}$ |
Cho khối chóp có diện tích đáy $B=a^2\sqrt{2}$ và chiều cao $h=2a$. Thể tích $V$ của khối chóp là
| $V=\dfrac{2a^3\sqrt{2}}{3}$ | |
| $V=\dfrac{2a^3\sqrt{2}}{9}$ | |
| $V=2a^3\sqrt{2}$ | |
| $V=\dfrac{a^3\sqrt{2}}{3}$ |
