Hàm số \(y=\sin^2x\cdot\left(1+\cos x\right)\) là hàm số

	chẵn
	lẻ
	không chẵn, không lẻ
	không có tính chẵn lẻ

Hai hàm số nào sau đây có chu kỳ tuần hoàn khác nhau?

	\(y=\cos x\) và \(y=\cot\dfrac{x}{2}\)
	\(y=\sin x\) và \(y=\tan2x\)
	\(y=\sin\dfrac{x}{2}\) và \(\cos\dfrac{x}{2}\)
	\(y=\tan2x\) và \(y=\cot2x\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=2\sin^2x+3\cos^23x.$$

	\(\mathscr{T}=\pi\)
	\(\mathscr{T}=2\pi\)
	\(\mathscr{T}=3\pi\)
	\(\mathscr{T}=\dfrac{\pi}{3}\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=2\cos^2x+2021.$$

	\(\mathscr{T}=3\pi\)
	\(\mathscr{T}=2\pi\)
	\(\mathscr{T}=\pi\)
	\(\mathscr{T}=4\pi\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=\sin\dfrac{x}{2}-\tan\left(2x+\dfrac{\pi}{4}\right).$$

	\(\mathscr{T}=4\pi\)
	\(\mathscr{T}=\pi\)
	\(\mathscr{T}=3\pi\)
	\(\mathscr{T}=2\pi\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=\tan3x+\cot x.$$

	\(\mathscr{T}=4\pi\)
	\(\mathscr{T}=\pi\)
	\(\mathscr{T}=3\pi\)
	\(\mathscr{T}=\dfrac{\pi}{3}\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=3\cos(2x+1)-2\sin\left(\dfrac{x}{2}-3\right).$$

	\(\mathscr{T}=4\pi\)
	\(\mathscr{T}=\pi\)
	\(\mathscr{T}=6\pi\)
	\(\mathscr{T}=3\pi\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=\sin\left(2x+\dfrac{\pi}{3}\right)+2\cos\left(3x-\dfrac{\pi}{4}\right).$$

	\(\mathscr{T}=2\pi\)
	\(\mathscr{T}=\pi\)
	\(\mathscr{T}=3\pi\)
	\(\mathscr{T}=4\pi\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=\cos3x+\cos5x.$$

	\(\mathscr{T}=\pi\)
	\(\mathscr{T}=3\pi\)
	\(\mathscr{T}=2\pi\)
	\(\mathscr{T}=5\pi\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=\cos2x+\sin\dfrac{x}{2}.$$

	\(\mathscr{T}=4\pi\)
	\(\mathscr{T}=\pi\)
	\(\mathscr{T}=2\pi\)
	\(\mathscr{T}=\dfrac{\pi}{2}\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số \(y=\tan3\pi x\).

	\(\mathscr{T}=\dfrac{\pi}{3}\)
	\(\mathscr{T}=\dfrac{4}{3}\)
	\(\mathscr{T}=\dfrac{2\pi}{3}\)
	\(\mathscr{T}=\dfrac{1}{3}\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=-\dfrac{1}{2}\sin\left(100\pi x+50\pi\right).$$

	\(\mathscr{T}=\dfrac{1}{50}\)
	\(\mathscr{T}=\dfrac{1}{100}\)
	\(\mathscr{T}=\dfrac{\pi}{50}\)
	\(\mathscr{T}=200\pi^2\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=\cos\left(\dfrac{x}{2}+2020\right).$$

	\(\mathscr{T}=4\pi\)
	\(\mathscr{T}=2\pi\)
	\(\mathscr{T}=-2\pi\)
	\(\mathscr{T}=\pi\)

Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=\sin\left(5x-\dfrac{\pi}{4}\right).$$

	\(\mathscr{T}=\dfrac{2\pi}{5}\)
	\(\mathscr{T}=\dfrac{5\pi}{2}\)
	\(\mathscr{T}=\dfrac{\pi}{2}\)
	\(\mathscr{T}=\dfrac{\pi}{8}\)

Trong các hàm số sau, hàm số nào không tuần hoàn?

	\(y=\cos x\)
	\(y=\cos2x\)
	\(y=x^2\cos x\)
	\(y=\dfrac{1}{\sin2x}\)

Trong các hàm số sau, hàm số nào là hàm số tuần hoàn?

	\(y=\sin x\)
	\(y=x+\sin x\)
	\(y=x\cos x\)
	\(y=\dfrac{\sin x}{x}\)

Mệnh đề nào sau đây là sai?

	Hàm số \(y=\sin x\) tuần hoàn với chu kì \(2\pi\)
	Hàm số \(y=\cos x\) tuần hoàn với chu kì \(2\pi\)
	Hàm số \(y=\tan x\) tuần hoàn với chu kì \(2\pi\)
	Hàm số \(y=\cot x\) tuần hoàn với chu kì \(\pi\)

Cho hàm số \(f\left(x\right)=\dfrac{x+m}{x+1}\) (\(m\) là tham số thực). Gọi \(S\) là tập hợp tất cả các giá trị của m sao cho $$\max\limits_{[0;1]}\left|f\left(x\right)\right|+\min\limits_{[0;1]}\left|f\left(x\right)\right|=2.$$Số phần tử của \(S\) là

	\(6\)
	\(2\)
	\(1\)
	\(4\)

Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:

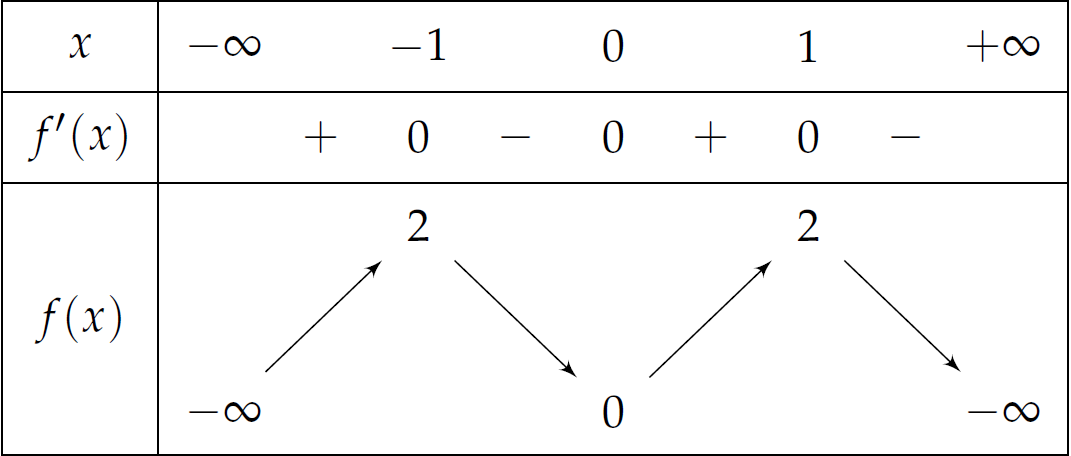
Số nghiệm thuộc đoạn \(\left[0;\dfrac{5\pi}{2}\right]\) của phương trình \(f\left(\sin x\right)=1\) là

	\(7\)
	\(4\)
	\(5\)
	\(6\)

Cho hàm số \(f\left(x\right)\) có \(f\left(0\right)=0\) và \(f'\left(x\right)=\cos x\cdot\cos^22x\), \(\forall x\in\mathbb{R}\). Khi đó \(\displaystyle\int\limits_0^{\pi}f\left(x\right)\mathrm{\,d}x\) bằng

	\(\dfrac{1042}{225}\)
	\(\dfrac{208}{225}\)
	\(\dfrac{242}{225}\)
	\(\dfrac{149}{225}\)