Dành cho lớp 11A4, hạn chót 4h chiều ngày 10/4/2023

Hãy chọn một bài toán trong số 9 bài toán dưới đây, trình bày bằng hình thức tự luận và chụp hình gửi vào phần bình luận ngay bên dưới.
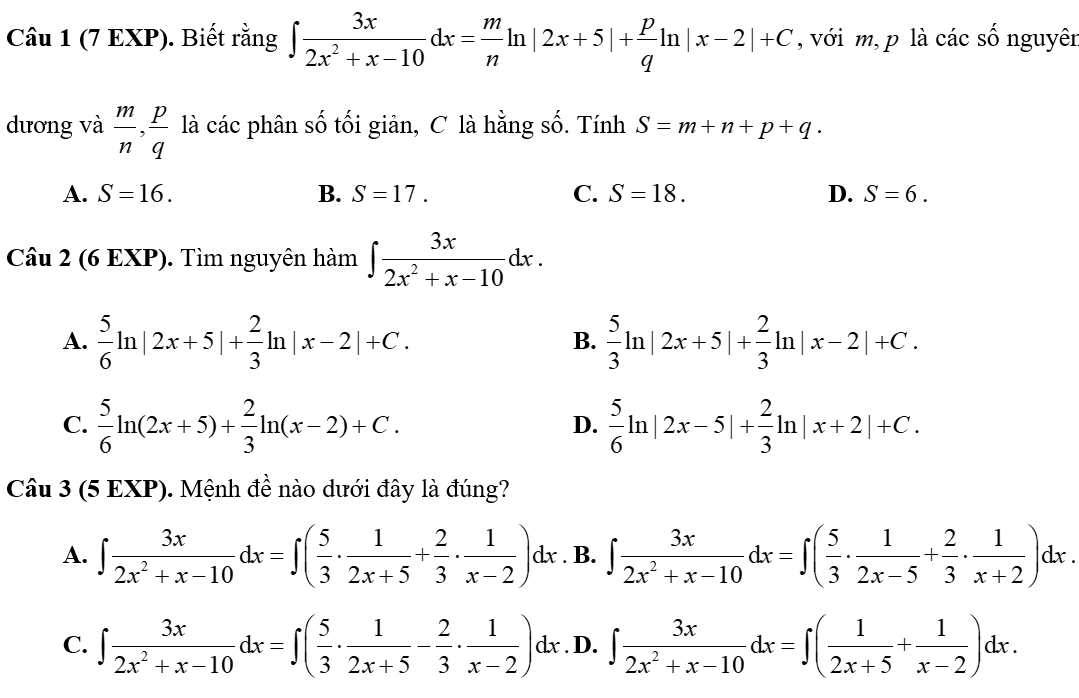


Dành cho nhóm 2
Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không đổi bằng $8$m$^3$, thùng tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng là $100.000$ đồng/m$^2$, giá tôn làm thành xung quanh thùng là $50.000$ đồng/m$^2$. Hỏi người bán gạo đó cần đóng thùng đựng gạo với cạnh đáy bằng bao nhiêu để chi phí mua nguyên liệu là nhỏ nhất?
- $3$m
- $1,5$m
- $2$m
- $1$m
Dành cho lớp 11A2
Cho hình chóp $S.ABCD$ có $ABCD$ là hình thang, đáy lớn $AD$. Tìm giao tuyến của $(SAB)$ và $(SCD)$.
Dành cho lớp 11A1
Cho hình chóp $S.ABCD$ có $ABCD$ là hình thang, đáy lớn $AD$. Tìm giao tuyến của $(SAB)$ và $(SCD)$.
