Trong mặt phẳng $Oxy$, cho hai điểm $M(2;0)$ và $N(0;2)$. Phép quay tâm $O$ biến điểm $M$ thành điểm $N$, khi đó góc quay là
| $\alpha=30^\circ$ | |
| $\alpha=90^\circ$ | |
| $\alpha=30^\circ$ hoặc $\alpha=45^\circ$ | |
| $\alpha=90^\circ$ hoặc $\alpha=270^\circ$ |
Trong mặt phẳng $Oxy$, cho các điểm $I(3;1)$ và $J(-1;-1)$. Tìm ảnh của $J$ qua phép quay $\mathrm{Q}_{(I,-90^\circ)}$.
| $J'(-3;3)$ | |
| $J'(1;-5)$ | |
| $J'(1;5)$ | |
| $J'(5;-3)$ |
Trong mặt phẳng $Oxy$, ảnh của đường tròn $(\mathscr{C})\colon(x+2)^2+(y-3)^2=9$ qua phép quay $\mathrm{Q}_{(O,90^\circ)}$ là đường tròn có phương trình
| $(x+2)^2+(y+3)^2=9$ | |
| $(x+3)^2+(y+2)^2=9$ | |
| $(x-3)^2+(y+2)^2=9$ | |
| $(x+2)^2+(y-3)^2=9$ |
Trong mặt phẳng $Oxy$, cho điểm $M(2;2)$. Trong bốn điểm sau, điểm nào là ảnh của $M$ qua phép quay tâm $O$ góc $-45^\circ$?
| $M'\left(2;-2\sqrt{2}\right)$ | |
| $M'\left(2\sqrt{2};2\right)$ | |
| $M'\left(0;2\sqrt{2}\right)$ | |
| $M'\left(2\sqrt{2};0\right)$ |
Trong mặt phẳng $Oxy$, ảnh của điểm $M(3;4)$ qua phép quay $\mathrm{Q}_{(O,45^\circ)}$ là
| $M'\left(\dfrac{7\sqrt{2}}{2};\dfrac{7\sqrt{2}}{2}\right)$ | |
| $M'\left(-\dfrac{\sqrt{2}}{2};\dfrac{7\sqrt{2}}{2}\right)$ | |
| $M'\left(-\dfrac{\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right)$ | |
| $M'\left(\dfrac{7\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right)$ |
Cho ngũ giác đều $ABCDE$ tâm $O$. Phép quay nào sau đây biến ngũ giác thành chính nó?
| $\mathrm{Q}_{(O,90^\circ)}$ | |
| $\mathrm{Q}_{(O,72^\circ)}$ | |
| $\mathrm{Q}_{(O,60^\circ)}$ | |
| $\mathrm{Q}_{(O,45^\circ)}$ |
Trong mặt phẳng $Oxy$, cho đường thẳng $d\colon y=x$. Tìm ảnh của $d$ qua phép quay tâm $O$ góc $90^\circ$.
| $d'\colon y=2x$ | |
| $d'\colon y=-x$ | |
| $d'\colon y=-2x$ | |
| $d'\colon y=x$ |
Trong mặt phẳng $Oxy$, cho đường thẳng $d\colon3x-y+2=0$. Tìm phương trình đường thẳng $d'$ là ảnh của $d$ qua phép quay tâm $O$ góc $-90^\circ$.
| $d'\colon3x-y-6=0$ | |
| $d'\colon x-3y-2=0$ | |
| $d'\colon x+3y-2=0$ | |
| $d'\colon x-3y+2=0$ |
Cho lục giác đều $ABCDEF$ tâm $O$ (như hình vẽ).
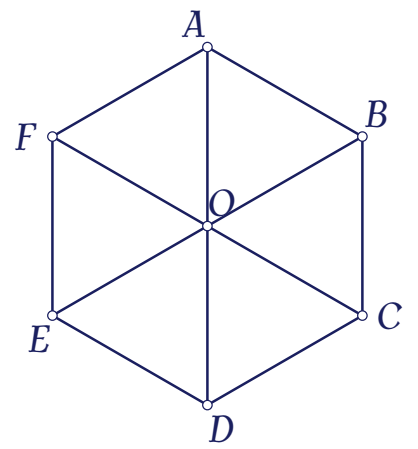
Tam giác $EOD$ là ảnh của tam giác $AOF$ qua phép quay tâm $O$ góc quay $\alpha$. Tìm số đo góc $\alpha$.
| $\alpha=60^\circ$ | |
| $\alpha=-60^\circ$ | |
| $\alpha=120^\circ$ | |
| $\alpha=-120^\circ$ |
Cho hình vuông $ABCD$ tâm $O$. Gọi $M,\,N,\,P,\,Q$ lần lượt là trung điểm của các cạnh $AB$, $BC$, $CD$, $DA$.
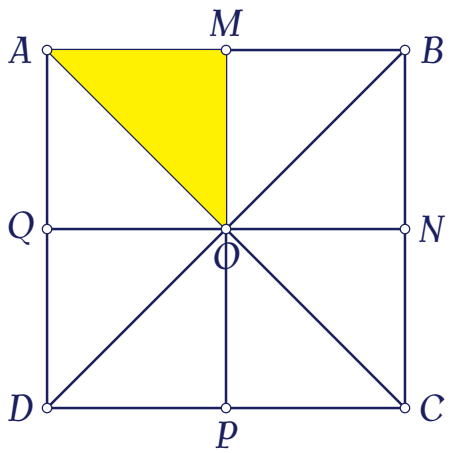
Ảnh của tam giác $OAM$ qua phép quay tâm $O$ góc $90^\circ$ là
| $\triangle ODQ$ | |
| $\triangle OBN$ | |
| $\triangle OAQ$ | |
| $\triangle OCN$ |
Trong mặt phẳng $Oxy$, cho điểm $B(-3;6)$. Tìm tọa độ điểm $E$ sao cho $B$ là ảnh của điểm $E$ qua phép quay tâm $O$ góc $-90^\circ$.
| $E(6;3)$ | |
| $E(-3;-6)$ | |
| $E(-6;-3)$ | |
| $E(3;6)$ |
Cho phép quay $\mathrm{Q}_{(O,\varphi)}$ biến điểm $A$ thành điểm $A'$ và biến điểm $M$ thành điểm $M'$. Mệnh đề nào sau đây là sai?
| $\overrightarrow{AM}=\overrightarrow{A'M'}$ | |
| $(OA,OA')=\widehat{(OM,OM')}=\varphi$ | |
| $\big(\overrightarrow{AM},\overrightarrow{AM'}\big)=\varphi$ với $0\leq\varphi\leq\pi$ | |
| $AM=A'M'$ |
Trong mặt phẳng $Oxy$, ảnh của điểm $M(-6;1)$ qua phép quay $\mathrm{Q}_{(O,-90^\circ)}$ là
| $M'(1;6)$ | |
| $M'(-1;-6)$ | |
| $M'(-6;-1)$ | |
| $M'(6;1)$ |
Trong mặt phẳng $Oxy$, phép quay tâm $O$ góc quay $90^\circ$ biến điểm $M(-1;2)$ thành điểm $M'$ có tọa độ là
| $(2;1)$ | |
| $(2;-1)$ | |
| $(-2;-1)$ | |
| $(-2;1)$ |
Cho hàm số $y=f(x)$ có đạo hàm $y=f'(x)$ với đồ thị như hình vẽ.
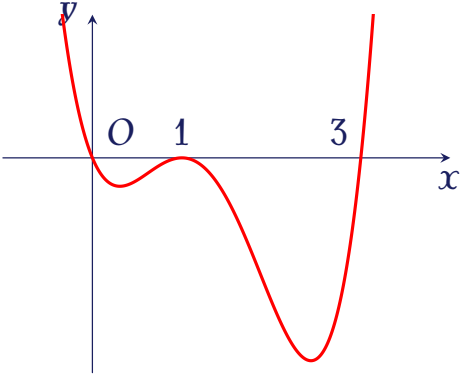
Tìm $m$ để hàm số $g(x)=f\big(x^2+m\big)$ có $3$ điểm cực trị.
| $m\in(-\infty;0]$ | |
| $m\in(3;+\infty)$ | |
| $m\in[0;3)$ | |
| $m\in(0;3)$ |
Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x-1)^2\big(x^2-2x\big)$ với $\forall x\in\mathbb{R}$. Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $f\big(x^2-8x+m\big)$ có $5$ điểm cực trị?
| $17$ | |
| $15$ | |
| $16$ | |
| $18$ |
Cho hàm số $y=f(x)$ có đạo hàm $y=f'(x)$ với đồ thị như hình vẽ.
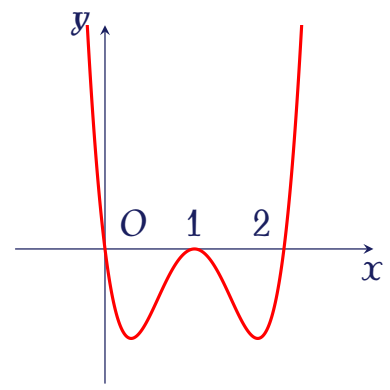
Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $g(x)=f\big(x^2-8x+m\big)$ có $5$ điểm cực trị.
| $15$ | |
| $16$ | |
| $17$ | |
| $18$ |
Trong mặt phẳng $Oxy$, cho hai đường thẳng song song $d\colon2x-3y-1=0$ và $d'\colon2x-3y+5=0$. Phép tịnh tiến theo vectơ nào sau đây không thể biến $d$ thành $d'$?
| $\overrightarrow{u}=(0;2)$ | |
| $\overrightarrow{u}=(-3;0)$ | |
| $\overrightarrow{u}=(3;4)$ | |
| $\overrightarrow{u}=(-1;1)$ |
Trong mặt phẳng $Oxy$, cho vectơ $\overrightarrow{v}=(-2;-1)$ và parabol $(\mathscr{P})\colon y=x^2$. Phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến $(\mathscr{P})$ thành parabol $(\mathscr{P}')$ có phương trình
| $y=x^2+4x+5$ | |
| $y=x^2+4x-5$ | |
| $y=x^2+4x+3$ | |
| $y=x^2-4x+5$ |
Trong mặt phẳng $Oxy$, cho hai đường thẳng song song $d\colon2x-y+4=0$ và $d'\colon2x-y+1=0$. Tìm giá trị thực của tham số $m$ để phép tịnh tiến theo vectơ $\overrightarrow{u}=(m;-3)$ biến đường thẳng $d$ thành đường thẳng $d'$.
| $m=1$ | |
| $m=2$ | |
| $m=3$ | |
| $m=4$ |
