Với $a$ là số thực dương tùy ý, $4\log\sqrt{a}$ bằng
| $-2\log a$ | |
| $2\log a$ | |
| $-4\log a$ | |
| $8\log a$ |
Tập xác định của hàm số $y=\log_3(x-4)$ là
| $(5;+\infty)$ | |
| $(-\infty;+\infty)$ | |
| $(4;+\infty)$ | |
| $(-\infty;4)$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
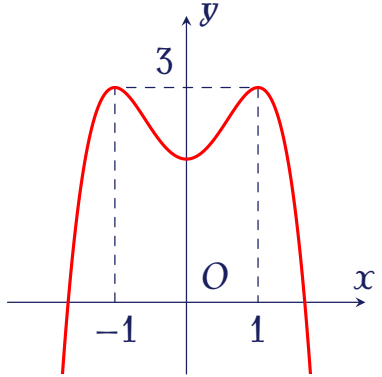
Số nghiệm thực của phương trình $f(x)=1$ là
| $1$ | |
| $2$ | |
| $4$ | |
| $3$ |
Môđun của số phức $z=3+4i$ bằng
| $25$ | |
| $\sqrt{7}$ | |
| $5$ | |
| $7$ |
Hàm số nào dưới đây có bảng biến thiên như hình vẽ?
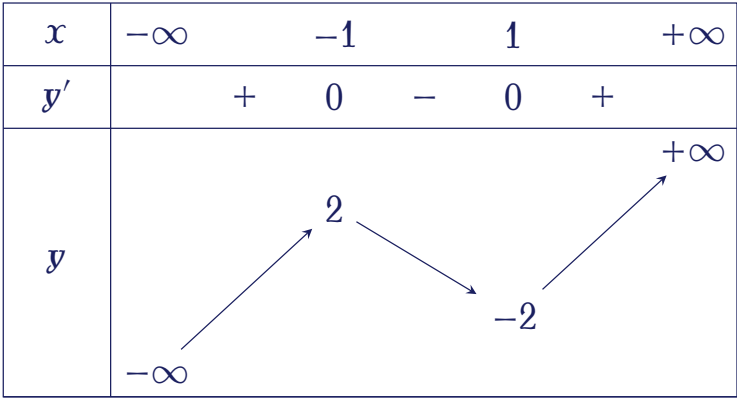
| $y=x^4-2x^2$ | |
| $y=-x^3+3x$ | |
| $y=-x^4+2x^2$ | |
| $y=x^3-3x$ |
Tập nghiệm của bất phương trình $\log_5(x+1)>2$ là
| $(9;+\infty)$ | |
| $(25;+\infty)$ | |
| $(31;+\infty)$ | |
| $(24;+\infty)$ |
Tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x-1}{2x+4}$ là đường thẳng có phương trình
| $x=-2$ | |
| $x=1$ | |
| $y=1$ | |
| $y=-2$ |
Cho hình trụ có chiều cao $h=1$ và bán kính đáy $r=2$. Diện tích xung quanh của hình trụ đã cho bằng
| $4\pi$ | |
| $2\pi$ | |
| $3\pi$ | |
| $6\pi$ |
Cho cấp số nhân $\big(u_n\big)$ với $u_1=1$ và $u_2=2$. Công bội của cấp số nhân đã cho là
| $q=\dfrac{1}{2}$ | |
| $q=2$ | |
| $q=-2$ | |
| $q=-\dfrac{1}{2}$ |
Cho khối chóp $S.ABC$ có chiều cao bằng $3$, đáy $ABC$ có diện tích bằng $10$. Thể tích khối chóp $S.ABC$ bằng
| $2$ | |
| $15$ | |
| $10$ | |
| $30$ |
Trong không gian $Oxyz$, cho điểm $A(1;2;-3)$. Hình chiếu vuông góc của $A$ lên mặt phẳng $(Oxy)$ có tọa độ là
| $(0;2;-3)$ | |
| $(1;0;-3)$ | |
| $(1;2;0)$ | |
| $(1;0;0)$ |
Trong không gian $Oxyz$, cho mặt cầu $(S)\colon x^2+(y-2)^2+(z+1)^2=6$. Đường kính của $(S)$ bằng
| $\sqrt{6}$ | |
| $12$ | |
| $2\sqrt{6}$ | |
| $3$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
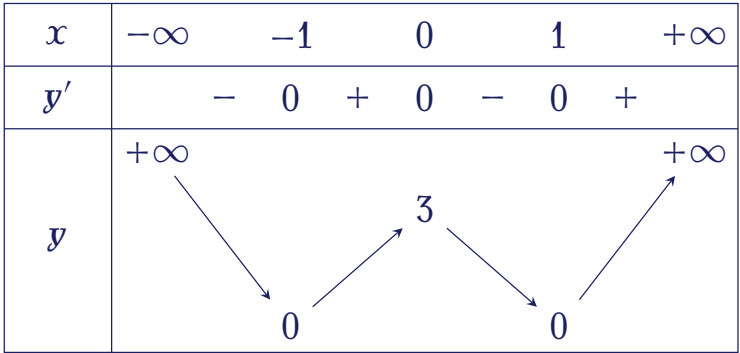
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(1;+\infty)$ | |
| $(0;1)$ | |
| $(-1;0)$ | |
| $(0;+\infty)$ |
Cho $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=-\cos x+C$. Khẳng định nào dưới đây đúng?
| $f(x)=-\sin x$ | |
| $f(x)=-\cos x$ | |
| $f(x)=\sin x$ | |
| $f(x)=\cos x$ |
Nếu $\displaystyle\displaystyle\int\limits_{-1}^{5}f(x)\mathrm{\,d}x=-3$ thì $\displaystyle\displaystyle\int\limits_{5}^{-1}f(x)\mathrm{\,d}x$ bằng
| $5$ | |
| $6$ | |
| $4$ | |
| $3$ |
Cho khối lăng trụ có diện tích đáy là $3a^2$ và chiều cao $2a$. Thể tích khối lăng trụ đã cho bằng
| $a^3$ | |
| $6a^3$ | |
| $3a^3$ | |
| $2a^3$ |
Nếu $\displaystyle\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x=4$ thì $\displaystyle\displaystyle\int\limits_{0}^{2}\left[\dfrac{1}{2}f(x)+2\right]\mathrm{\,d}x$ bằng
| $6$ | |
| $8$ | |
| $4$ | |
| $2$ |
Cho một hộp kín có chứa $3$ bi đỏ, $4$ bi xanh, $5$ bi vàng. Lấy ngẫu nhiên $4$ viên bi. Tính xác suất để $4$ viên bi lấy ra không có bi màu đỏ.
Cho $3$ tấm bìa khác nhau trên đó đã được viết lên các chữ cái $K,Y,S$. Sau đó người ta thử trải ra ngẫu nhiên thành hàng ngang, hãy mô tả không gian mẫu của phép thử trên.
Tìm hệ số của $x^{2012}$ trong khai triển của nhị thức $\left(x^2-\dfrac{2}{x^3}\right)^{2011}$ với $x\neq0$.
