Cho lục giác đều \(ABCDEF\) có tâm \(O\).

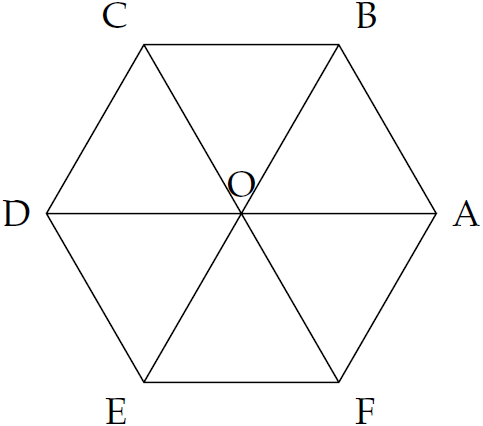
Có bao nhiêu vectơ (khác \(\vec{0}\)) ngược hướng với vectơ \(\overrightarrow{OB}\) mà có điểm đầu và điểm cuối là một trong các đỉnh và tâm của \(ABCDEF\)?

	\(3\)
	\(9\)
	\(5\)
	\(4\)

Cho lục giác đều \(ABCDEF\) có tâm \(O\). Có bao nhiêu vectơ (khác \(\vec{0}\)) cùng phương với vectơ \(\overrightarrow{OC}\) mà có điểm đầu và điểm cuối là một trong các đỉnh và tâm của \(ABCDEF\)?

	\(4\)
	\(6\)
	\(7\)
	\(9\)

Cho tam giác \(ABC\). Gọi \(M,\,N\) lần lượt là trung điểm của các cạnh \(AB,\,AC\). Cặp vectơ nào sau đây cùng hướng?

	\(\overrightarrow{MN}\) và \(\overrightarrow{CB}\)
	\(\overrightarrow{AB}\) và \(\overrightarrow{MB}\)
	\(\overrightarrow{MA}\) và \(\overrightarrow{MB}\)
	\(\overrightarrow{AN}\) và \(\overrightarrow{CA}\)

Cho \(\overrightarrow{AB}=\overrightarrow{AC}\). Chọn phát biểu sai.

	\(AB=AC\)
	\(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng hướng
	\(B\equiv C\)
	\(B\neq C\)

Cho tam giác \(ABC\). Cặp vectơ nào sau đây cùng phương?

	\(\overrightarrow{AB}\) và \(\overrightarrow{AC}\)
	\(\overrightarrow{AB}\) và \(\overrightarrow{BC}\)
	\(\overrightarrow{AC}\) và \(\overrightarrow{BC}\)
	\(\overrightarrow{AB}\) và \(\overrightarrow{BA}\)

Chọn mệnh đề đúng trong các mệnh đề sau?

	Hai vectơ có giá song song thì cùng phương
	Hai vectơ không cùng phương thì ngược hướng
	Hai vectơ không cùng phương thì cắt nhau
	Hai vectơ có cùng độ dài thì bằng nhau

Vectơ nào sau đây không phải là vectơ \(\vec{0}\)?

	\(\overrightarrow{AB}\)
	\(\overrightarrow{AA}\)
	\(\overrightarrow{BB}\)
	\(\overrightarrow{CC}\)

Mệnh đề nào dưới đây đúng?

	Hai vectơ (khác \(\vec{0}\)) bằng nhau thì không bao giờ cùng phương
	Hai vectơ bằng nhau thì chúng phải có điểm đầu và điểm cuối trùng nhau
	Hai vectơ (khác \(\vec{0}\)) cùng phương thì song song
	Hai vectơ bằng nhau thì cùng hướng

Trong các khẳng định sau, khẳng định nào đúng?

	Vectơ là một đường thẳng có hướng
	Vectơ là một đường thẳng
	Vectơ là một đoạn thẳng có hướng
	Vectơ là một đoạn thẳng

Khẳng định nào sau đây đúng?

	Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương
	Hai vectơ cùng phương với một vectơ thứ ba khác \(\vec{0}\) thì cùng phương
	Hai vectơ ngược hướng với một vectơ thứ ba thì ngược hướng
	Hai vectơ bằng nhau khi và chỉ khi chúng có độ dài bằng nhau

Cho vectơ \(\overrightarrow{AB}\neq\vec{0}\) và một điểm \(C\). Có bao nhiêu điểm \(D\) thỏa mãn \(\overrightarrow{AB}=\overrightarrow{CD}\)?

	Vô số
	Không có
	\(1\) điểm
	\(2\) điểm

Phát biểu nào sau đây là sai?

	Hai vectơ cùng hướng thì cùng phương
	Hai vectơ ngược hướng thì cùng phương
	Hai vectơ ngược hướng thì không cùng phương
	Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối

Phát biểu nào sau đây là sai?

	Vectơ là đoạn thẳng có hướng
	Hai vectơ cùng hướng thì cùng phương
	Vectơ \(\vec{0}\) cùng phương với mọi vectơ
	Hai vectơ cùng phương thì cùng hướng

Tứ giác \(ABCD\) là hình bình hành khi và chỉ khi

	\(\overrightarrow{AC}=\overrightarrow{BD}\)
	\(\overrightarrow{BC}=\overrightarrow{DA}\)
	\(\overrightarrow{BA}=\overrightarrow{CD}\)
	\(\overrightarrow{AB}=\overrightarrow{CD}\)

Cho bốn điểm phân biệt \(A,\,B,\,C,\,D\) mà trong đó không có ba điểm nào thẳng hàng. Điều kiện cần và đủ để \(\overrightarrow{AB}=\overrightarrow{CD}\) là

	\(ABCD\) là hình bình hành
	\(ABDC\) là hình bình hành
	\(AC=BD\)
	\(AB=CD\)

Hai vectơ được gọi là bằng nhau khi và chỉ khi

	Giá của chúng trùng nhau và độ dài của chúng bằng nhau
	Chúng trùng với một trong các cặp cạnh đối của một hình bình hành
	Chúng trùng với một trong các cặp cạnh đối của một tam giác đều
	Chúng cùng hướng và độ dài bằng nhau

Mệnh đề nào sau đây sai?

	\(\overrightarrow{AA}=\vec{0}\)
	\(\vec{0}\) cùng hướng với mọi vectơ
	\(\left|\overrightarrow{AB}\right|>0\)
	\(\vec{0}\) cùng phương với mọi vectơ

Cho vectơ \(\overrightarrow{DE}\) khác \(\vec{0}\). Độ dài đoạn thẳng \(ED\) được gọi là

	Phương của \(\overrightarrow{ED}\)
	Hướng của \(\overrightarrow{ED}\)
	Giá của \(\overrightarrow{ED}\)
	Độ dài của \(\overrightarrow{ED}\)

Cho ba điểm \(A,\,B,\,C\) phân biệt. Khi đó

	Điều kiện cần và đủ để \(A,\,B,\,C\) thẳng hàng là \(\overrightarrow{AB}\) cùng phương với \(\overrightarrow{AC}\)
	Điều kiện đủ để \(A,\,B,\,C\) thẳng hàng là \(\overrightarrow{MA}\) cùng phương với \(\overrightarrow{AB}\) với mọi \(M\)
	Điều kiện cần để \(A,\,B,\,C\) thẳng hàng là \(\overrightarrow{MA}\) cùng phương với \(\overrightarrow{AB}\) vói mọi \(M\)
	Điều kiện cần để \(A,\,B,\,C\) thẳng hàng là \(\overrightarrow{AB}=\overrightarrow{AC}\)

Mệnh đề nào sau đây đúng?

	Có duy nhất một vectơ cùng phương với mọi vectơ
	Có ít nhất hai vectơ có cùng phương với mọi vectơ
	Có vô số vectơ cùng phương với mọi vectơ
	Không có vectơ nào cùng phương với mọi vectơ