Gọi tam giác cong \(OAB\) là hình phẳng giới hạn bởi đồ thị các hàm số \(y=2x^2\), \(y=3-x\), \(y=0\) (như hình vẽ).

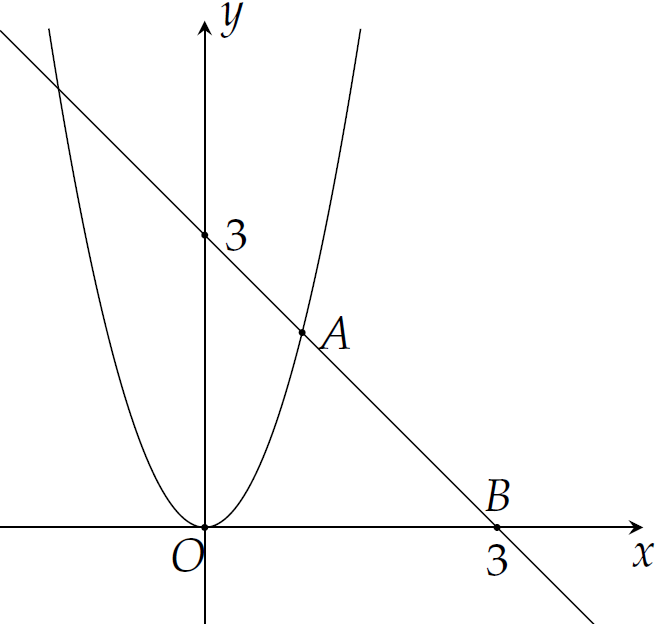
Tính diện tích \(S\) của tam giác cong \(OAB\).

	\(S=\dfrac{8}{3}\)
	\(S=\dfrac{4}{3}\)
	\(S=\dfrac{5}{3}\)
	\(S=\dfrac{10}{3}\)

Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^2\), \(y=\dfrac{x^2}{8}\), \(y=\dfrac{27}{x}\).

	\(\dfrac{63}{8}\)
	\(27\ln2-\dfrac{63}{8}\)
	\(27\ln2\)
	\(27\ln2-\dfrac{63}{4}\)

Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^2\), \(y=-\dfrac{1}{3}x+\dfrac{4}{3}\) và trục hoành như hình vẽ.

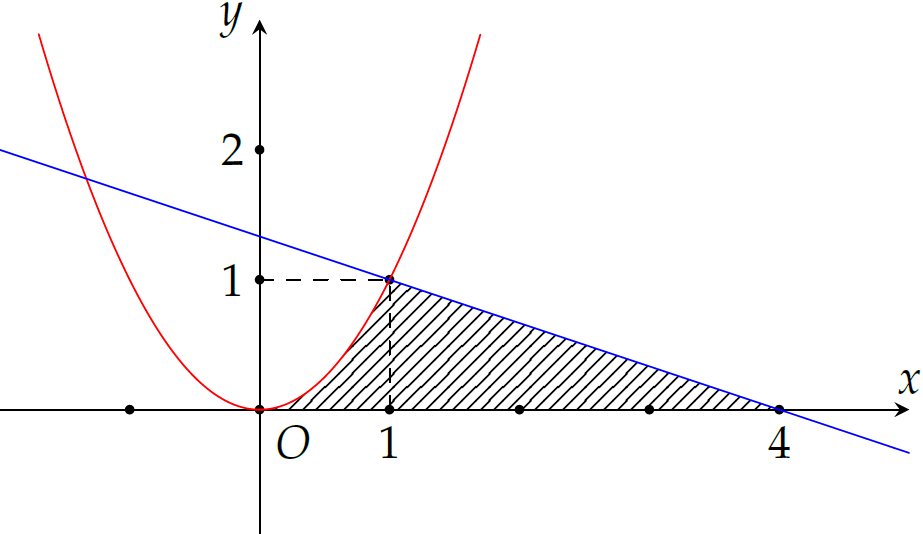
	\(\dfrac{7}{3}\)
	\(\dfrac{56}{3}\)
	\(\dfrac{39}{2}\)
	\(\dfrac{11}{6}\)

Tính diện tích phần hình phẳng gạch chéo (tam giác cong \(OAB\)) trong hình vẽ.

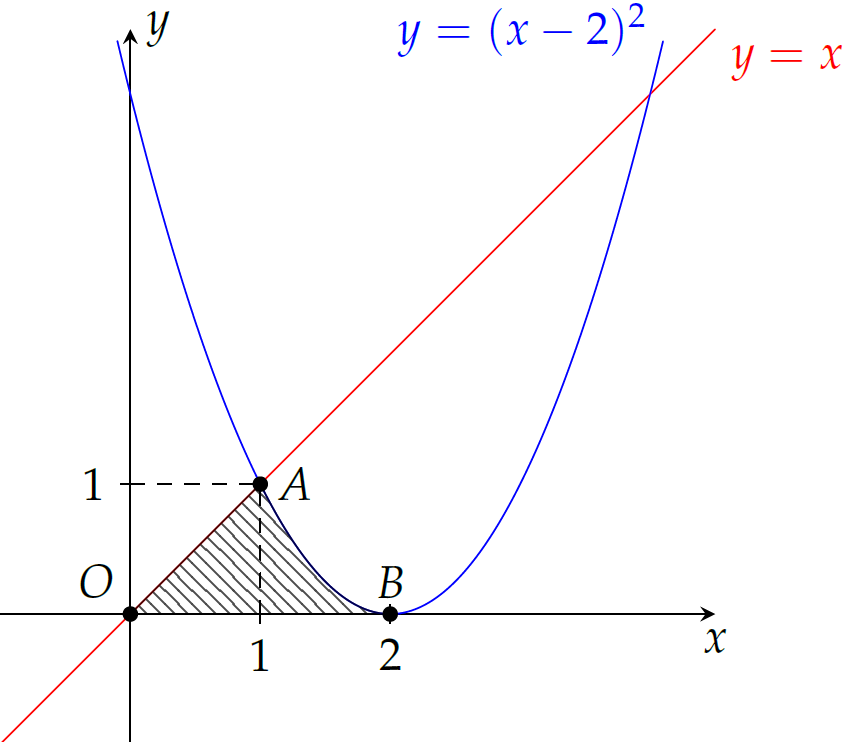
	\(\dfrac{5}{6}\)
	\(\dfrac{5\pi}{6}\)
	\(\dfrac{8}{15}\)
	\(\dfrac{8\pi}{15}\)

Diện tích của hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\), \(y=2-x\) và trục hoành bằng

	\(\dfrac{5}{6}\)
	\(\dfrac{5\pi}{6}\)
	\(\dfrac{7}{6}\)
	\(\dfrac{7\pi}{6}\)

Tính diện tích \(S\) của hình phẳng (phần gạch sọc) trong hình.

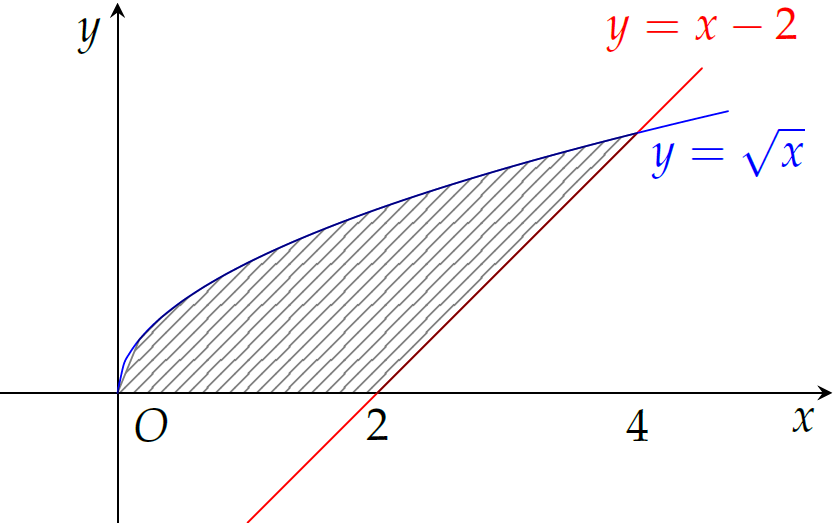
	\(S=\dfrac{8}{3}\)
	\(S=\dfrac{10}{3}\)
	\(S=\dfrac{11}{3}\)
	\(S=\dfrac{7}{3}\)

Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y=\dfrac{x+1}{x+2}\), trục hoành và đường thẳng \(x=2\) là

	\(3+\ln2\)
	\(3-\ln2\)
	\(3+2\ln2\)
	\(3-2\ln2\)

Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=-x^3+3x^2-4\) và trục hoành.

	\(S=\dfrac{27}{4}\)
	\(S=\dfrac{27\pi}{4}\)
	\(S=4\)
	\(S=1\)

Tính diện tích hình phẳng giới hạn bởi hai đường cong \(y=x^3-x\) và \(y=x-x^2\).

	\(\dfrac{5}{12}\)
	\(\dfrac{37}{12}\)
	\(\dfrac{8}{3}\)
	\(\dfrac{9}{4}\)

Tính diện tích miền phẳng giới hạn bởi các đường \(y=x^3+2x+1\), trục hoành, \(x=1\) và \(x=2\).

	\(\dfrac{31}{4}\)
	\(\dfrac{49}{4}\)
	\(\dfrac{21}{4}\)
	\(\dfrac{39}{4}\)

Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y=x^3-12x\) và \(y=x^2\) là

	\(S=\dfrac{939}{12}\)
	\(S=\dfrac{979}{12}\)
	\(S=\dfrac{160}{3}\)
	\(S=\dfrac{937}{12}\)

Cho \(a\) là số thực thỏa mãn \(|a|<2\) và \(\displaystyle\int\limits_a^2(2x+1)\mathrm{\,d}x=4\). Giá trị biểu thức \(1+a^3\) bằng

	\(0\)
	\(2\)
	\(1\)
	\(3\)

Cho \(M\), \(N\) là các số thực, xét hàm số \(f(x)=M\sin\pi x+N\cos\pi x\) thỏa mãn \(f(1)=3\) và \(\displaystyle\int\limits_0^{\tfrac{1}{2}}f(x)\mathrm{\,d}x=-\dfrac{1}{\pi}\). Giá trị của \(f'\left(\dfrac{1}{4}\right)\) bằng

	\(\dfrac{5\pi\sqrt{2}}{2}\)
	\(-\dfrac{5\pi\sqrt{2}}{2}\)
	\(-\dfrac{\pi\sqrt{2}}{2}\)
	\(\dfrac{\pi\sqrt{2}}{2}\)

Tích phân \(\displaystyle\int\limits_0^13^{2x+1}\mathrm{\,d}x\) bằng

	\(\dfrac{27}{\ln9}\)
	\(\dfrac{9}{\ln9}\)
	\(\dfrac{4}{\ln3}\)
	\(\dfrac{12}{\ln3}\)

Tính tích phân \(I=\displaystyle\int\limits_0^{\tfrac{\pi}{2}}\left(\sin{2x}+\sin x\right)\mathrm{\,d}x\).

	\(5\)
	\(3\)
	\(4\)
	\(2\)

Nếu các số hữu tỉ \(a\), \(b\) thỏa mãn \(\displaystyle\int\limits_0^1 \left(a\mathrm{e}^x+b\right)\mathrm{\,d}x=\mathrm{e}+2\) thì giá trị của biểu thức \(a+b\) bằng

	\(4\)
	\(5\)
	\(6\)
	\(3\)

Biết \(\displaystyle\int\limits_1^2\dfrac{4\mathrm{\,d}x}{(x+4)\sqrt{x}+x\sqrt{x+4}}=\sqrt{a}+\sqrt{b}-\sqrt{c}-d\) với \(a\), \(b\), \(c\), \(d\) là các số nguyên dương. Tính \(P=a+b+c+d\).

	\(48\)
	\(46\)
	\(54\)
	\(52\)

Biết \(I=\displaystyle\int\limits_1^2\dfrac{dx}{\left(2x+2\right)\sqrt{x}+2x\sqrt{x+1}}=\dfrac{\sqrt{a}-\sqrt{b}-c}{2}\) với \(a\), \(b\), \(c\) là các số nguyên dương. Tính \(P=a-b+c\).

	\(P=24\)
	\(P=12\)
	\(P=18\)
	\(P=22\)

Biết \(\displaystyle\int\limits_1^3\dfrac{\mathrm{\,d}x}{\sqrt{x+1}-\sqrt{x}}=a\sqrt{3}+b\sqrt{2}+c\) với \(a\), \(b\), \(c\) là các số hữu tỷ. Tính \(P =a+b+c\).

	\(P=\dfrac{13}{2}\)
	\(P=\dfrac{16}{3}\)
	\(P=5\)
	\(P=\dfrac{2}{3}\)

Biết \(\displaystyle\int\limits_0^1\dfrac{x}{\sqrt{x+1}}\mathrm{\,d}x=\dfrac{a}{b}\left(c-\sqrt{2}\right)\) với \(\dfrac{a}{b}\) là phân số tối giản. Tính \(a+b+c\).

	\(-1\)
	\(7\)
	\(3\)
	\(1\)