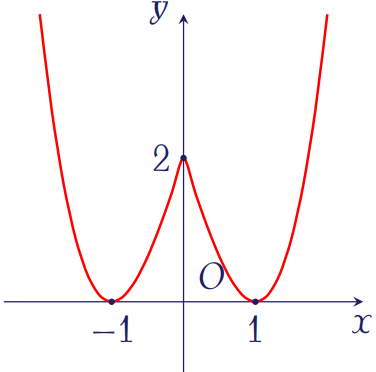
Đồ thị như hình trên là của hàm số nào sau đây?

	\(y=x^4-2x^2+2\)
	\(y=2\left(x^2-1\right)^2\)
	\(y=|x|^3-3|x|+2\)
	\(y=x^2-2|x|^2+2\)

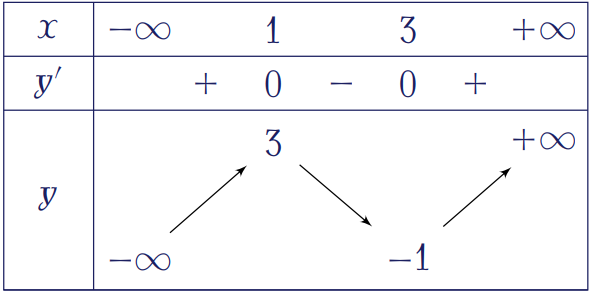
Bảng biến thiên trong hình trên là của hàm số nào sau đây?

	\(y=x^3-5x^2+x+6\)
	\(y=x^3-6x^2+9x-1\)
	\(y=-x^3+6x^2-9x+7\)
	\(y=x^4+x^2-3\)

Đồ thị hàm số \(y=\dfrac{x+1}{1-x}\) là hình nào sau đây?

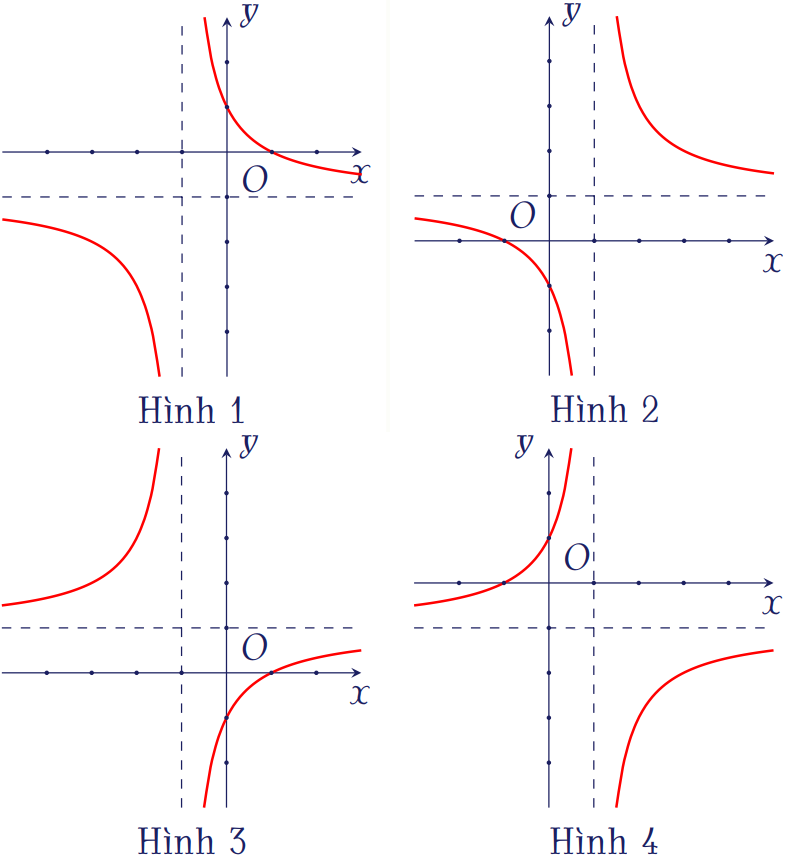
	Hình 1
	Hình 2
	Hình 3
	Hình 4

Đồ thị hàm số \(y=-x^3-3x^2+2\) là hình nào sau đây?

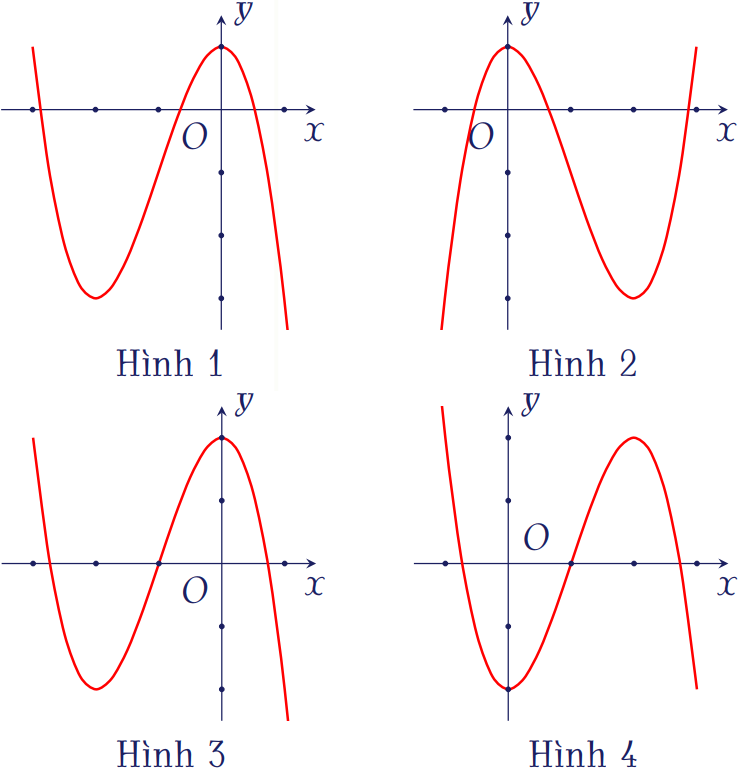
	Hình 1
	Hình 2
	Hình 3
	Hình 4

Đồ thị nào sau đây không thể là đồ thị hàm số \(y=ax^4+bx^2+c\) với \(a,\,b,\,c\) là các số thực và \(a\neq0\)?

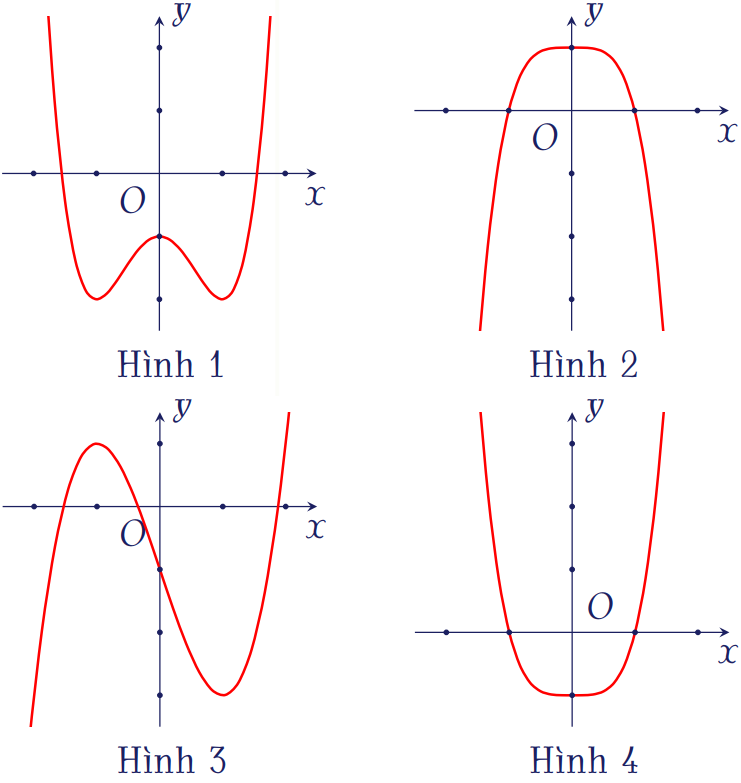
	Hình 1
	Hình 2
	Hình 3
	Hình 4

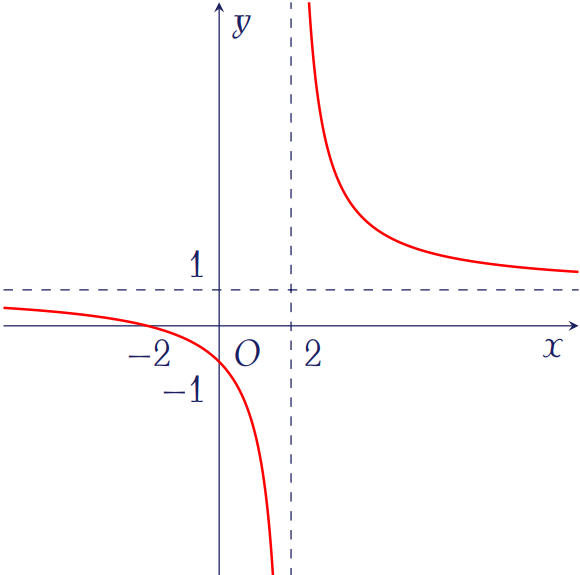
Đồ thị như hình bên là của hàm số nào sau đây?

	\(y=\dfrac{2x+1}{x-1}\)
	\(y=\dfrac{x+2}{x-2}\)
	\(y=\dfrac{x+2}{x+1}\)
	\(y=\dfrac{x-1}{x+1}\)

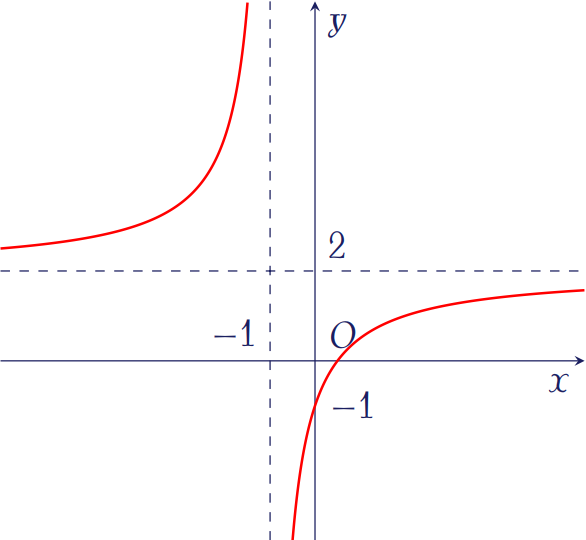
Hàm số \(y=f(x)\) có đồ thị như hình vẽ là hàm số nào sau đây?

	\(y=\dfrac{2x+1}{x-1}\)
	\(y=\dfrac{2x-1}{x-1}\)
	\(y=\dfrac{2x-1}{x+1}\)
	\(y=\dfrac{3x+1}{2x+2}\)

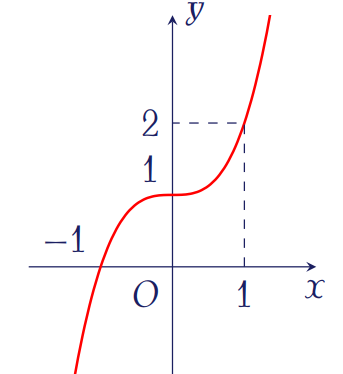
Đồ thị trong hình vẽ bên là của hàm số

	\(y=2x^3+1\)
	\(y=x^3+x+1\)
	\(y=x^3+1\)
	\(y=-x^3+2x+1\)

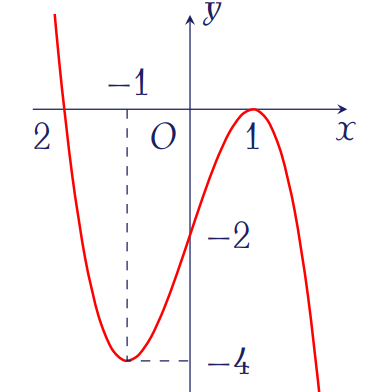
Đường cong như hình bên là đồ thị của hàm số nào dưới đây?

	\(y=x^3-3x-2\)
	\(y=-x^3+3x+2\)
	\(y=x^3-3x+2\)
	\(y=-x^3+3x-2\)

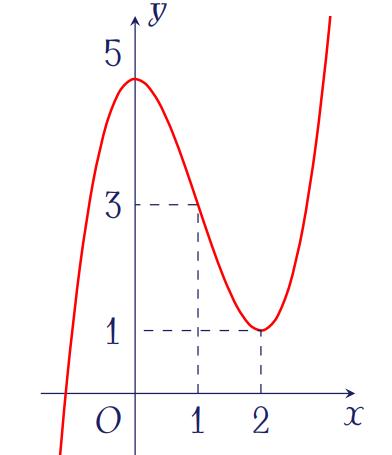
Đường cong như hình bên là đồ thị của hàm số nào?

	\(y=-x^3+3x^2+5\)
	\(y=2x^3-6x^2+5\)
	\(y=x^3-3x^2+5\)
	\(y=x^3-3x+5\)

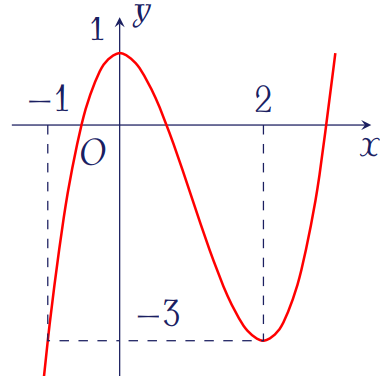
Đồ thị trong hình vẽ bên là của hàm số

	\(y=-\dfrac{x^3}{4}+x^2+1\)
	\(y=x^3+3x^2+1\)
	\(y=-x^3+3x^2+1\)
	\(y=x^3-3x^2+1\)

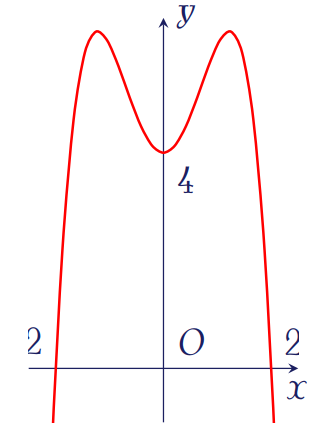
Đồ thị trong hình vẽ bên là của hàm số

	\(y=-x^2+x-4\)
	\(y=x^4-3x^2-4\)
	\(y=-x^3+2x^2+4\)
	\(y=-x^4+3x^2+4\)

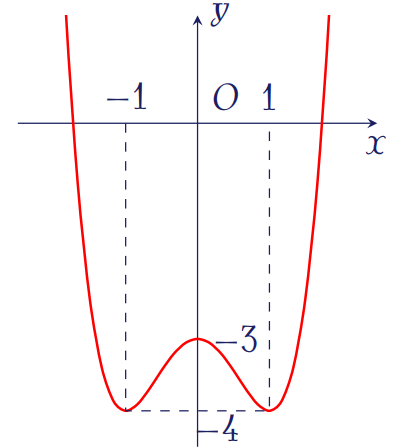
Đường cong trong hình vẽ bên là của hàm số nào sau đây?

	\(y=-x^3+x^2-2\)
	\(y=-x^4+3x^2-2\)
	\(y=x^4-2x^2-3\)
	\(y=-x^2+x-1\)

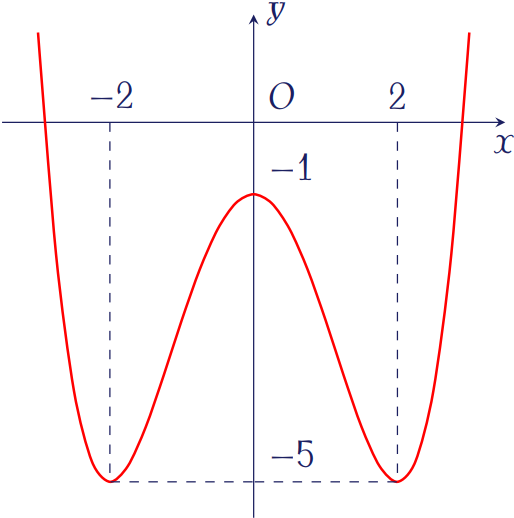
Đồ thị trong hình vẽ bên là của hàm số

	\(y=\dfrac{x^4}{4}-\dfrac{x^2}{2}-1\)
	\(y=\dfrac{x^4}{4}-x^2-1\)
	\(y=\dfrac{x^4}{4}-2x^2-1\)
	\(y=-\dfrac{x^4}{4}+x^2-1\)

Đồ thị hàm số nào dưới đây có tiệm cận đứng \(x=1\) và đi qua điểm \(A(2;5)\)?

	\(y=\dfrac{2-3x}{1-x}\)
	\(y=\dfrac{x+13}{x+1}\)
	\(y=\dfrac{2x+1}{x-1}\)
	\(y=\dfrac{x+1}{x-1}\)

Tìm giao điểm của hai đường tiệm cận của đồ thị hàm số \(y=\dfrac{x-2}{x+2}\).

	\(M(2;1)\)
	\(N(-2;2)\)
	\(P(-2;-2)\)
	\(Q(-2;1)\)

Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số \(y=\dfrac{3x-7}{x+2}\) là

	\((2;-3)\)
	\((-2;3)\)
	\((3;-2)\)
	\((-3;2)\)

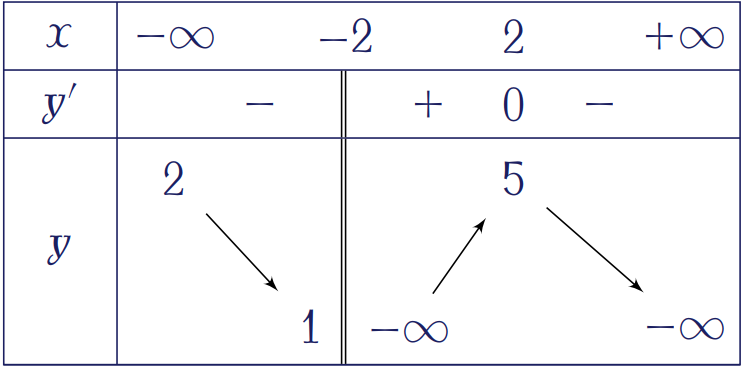
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

	\(4\)
	\(2\)
	\(3\)
	\(1\)

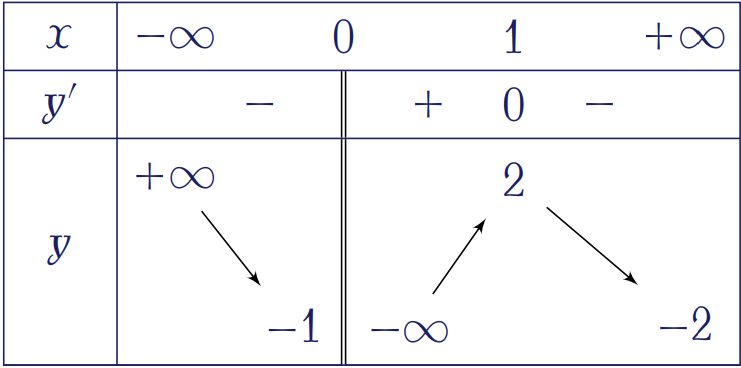
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

	\(3\)
	\(4\)
	\(1\)
	\(2\)

Cho hàm số \(y=f(x)\) có bảng biến thiên như hình bên. Đồ thị của \(f(x)\) có

	\(2\) đường tiệm cận đứng là \(x=2\) và \(x=-4\)
	\(2\) đường tiệm cận ngang là \(y=2\) và \(y=-4\)
	\(2\) đường tiệm cận ngang là \(x=2\) và \(x=-4\)
	\(2\) đường tiệm cận đứng là \(y=2\) và \(y=-4\)