Trong không gian \(Oxyz\), cho tứ diện \(ABCD\) có \(A(0;2;0)\), \(B(2;0;0)\), \(C\left(0;0;\sqrt{2}\right)\) và \(D(0;-2;0)\). Tính số đo góc của hai mặt phẳng \((ABC)\) và \((ACD)\).

	\(30^\circ\)
	\(45^\circ\)
	\(60^\circ\)
	\(90^\circ\)

Trong không gian \(Oxyz\), cho hai mặt phẳng \((P)\colon2x-y-2z-9=0\) và \((Q)\colon x-y-6=0\). Số đo góc tạo bởi hai mặt phẳng bằng

	\(30^\circ\)
	\(45^\circ\)
	\(60^\circ\)
	\(90^\circ\)

Trong không gian \(Oxyz\), cho hai mặt phẳng \((P)\colon2x-y-z-3=0\) và \((Q)\colon x-z-2=0\). Tính số đo góc giữa hai mặt phẳng \((P)\) và \((Q)\).

	\(\left((P),(Q)\right)=30^\circ\)
	\(\left((P),(Q)\right)=45^\circ\)
	\(\left((P),(Q)\right)=60^\circ\)
	\(\left((P),(Q)\right)=90^\circ\)

Cho \((H)\) là hình phẳng giới hạn bởi parabol \(y=2x^2-1\) và nửa đường tròn có phương trình \(y=\sqrt{2-x^2}\) với \(-\sqrt{2}\leq x\leq\sqrt{2}\) (phần gạch chéo trong hình vẽ).

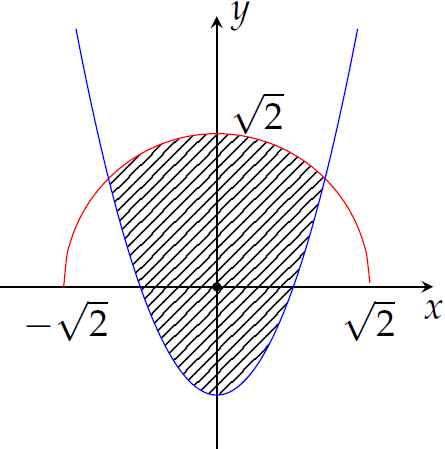
Diện tích của hình \((H)\) bằng

	\(\dfrac{3\pi-2}{6}\)
	\(\dfrac{3\pi+10}{3}\)
	\(\dfrac{3\pi+2}{6}\)
	\(\dfrac{3\pi+10}{6}\)

Tính diện tích hình phẳng giới hạn bởi parabol \(y=-x^2+2x\) và đường thẳng \(y=-3x\).

	\(S=\dfrac{125}{2}\)
	\(S=\dfrac{125}{3}\)
	\(S=\dfrac{125}{6}\)
	\(S=\dfrac{125}{8}\)

Tính diện tích hình phẳng giới hạn bởi parabol \(y=x^2\) và đường thẳng \(y=2x\).

	\(S=\dfrac{5}{3}\)
	\(S=\dfrac{14}{3}\)
	\(S=\dfrac{20}{3}\)
	\(S=\dfrac{4}{3}\)

Diện tích hình phẳng giới hạn bởi hai đường parabol \(y=x^2-2x\) và \(y=2x^2-x-2\) là

	\(\dfrac{9}{2}\)
	\(9\)
	\(5\)
	\(4\)

Tính diện tích \(S\) của phần hình phẳng giới hạn bởi hai đồ thị hàm số \(y=x^3-3x^2\) và \(y=x^2+x-4\).

	\(S=\dfrac{253}{12}\)
	\(S=\dfrac{125}{12}\)
	\(S=\dfrac{16}{3}\)
	\(S=\dfrac{63}{4}\)

Cho \((H)\) là hình phẳng giới hạn bởi các đường \(y=\sqrt{2x}\), \(y=2x-2\) và trục hoành. Tính diện tích của \((H)\).

	\(S=\dfrac{5}{3}\)
	\(S=\dfrac{16}{3}\)
	\(S=\dfrac{10}{3}\)
	\(S=\dfrac{8}{3}\)

Tính diện tích \(S\) của hình phẳng giới hạn bởi elip \((E)\) có phương trình \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), với \(a,\,b>0\).

	\(S=\pi\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2\)
	\(S=\pi(a+b)^2\)
	\(S=\pi ab\)
	\(S=\dfrac{\pi a^2b^2}{a+b}\)

Diện tích \(S\) của hình phẳng giới hạn bởi đường cong \(y=-x^3+3x^2-2\), trục hoành và hai đường thẳng \(x=0\), \(x=2\) là

	\(S=\dfrac{5}{2}\)
	\(S=\dfrac{3}{2}\)
	\(S=\dfrac{7}{2}\)
	\(S=4\)

Gọi \(S\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành, \(x=a\), \(x=b\).

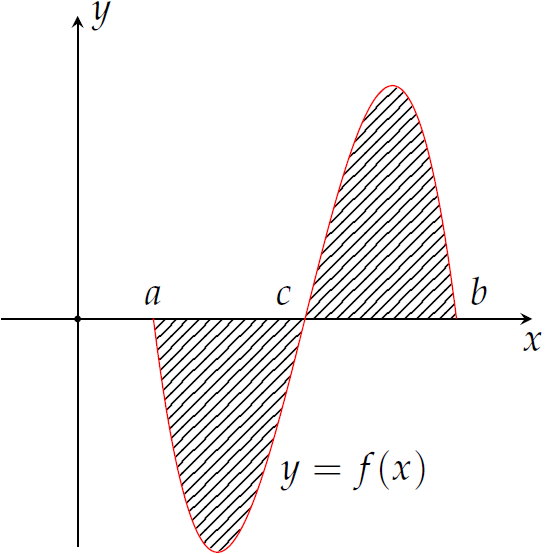
Khi đó \(S\) được tính theo công thức nào dưới đây?

	\(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\)
	\(S=-\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\)
	\(S=\left|\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\right|\)

Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y=f(x)\), trục hoành và hai đường thẳng \(x=-1\), \(x=2\) (như hình vẽ).

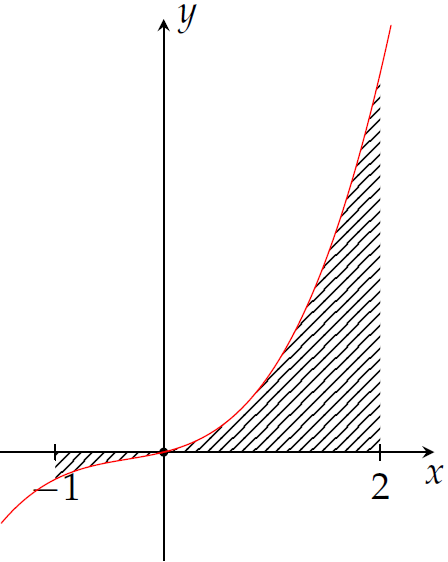
Đặt \(a=\displaystyle\int\limits_{-1}^{0}f(x)\mathrm{\,d}x\), \(b=\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x\), mệnh đề nào dưới đây đúng?

	\(S=b-a\)
	\(S=b+a\)
	\(S=a-b\)
	\(S=-a-b\)

Cho hai hàm số \(y=f_1(x)\) và \(y=f_2(x)\) liên tục trên đoạn \([a;b]\). Diện tích hình phẳng \(S\) giới hạn bởi các đường cong \(y=f_1(x)\), \(y=f_2(x)\) và các đường thẳng \(x=a\), \(x=b\) (\(a<b\)) được xác định bởi công thức nào sau đây?

	\(S=\displaystyle\int\limits_{a}^{b}\left|f_1(x)+f_2(x)\right|\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{b}\left[f_1(x)-f_2(x)\right]\mathrm{\,d}x\)
	\(S=\left|\displaystyle\int\limits_{a}^{b}\left[f_1(x)-f_2(x)\right]\mathrm{\,d}x\right|\)
	\(S=\displaystyle\int\limits_{a}^{b}\left|f_1(x)-f_2(x)\right|\mathrm{\,d}x\)

Cho hai hàm số \(y=f(x)\) và \(y=g(x)\) lên tục trên đoạn \([a;b]\). Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hai hàm số và hai đường thẳng \(x=a\), \(x=b\) (\(a< b\)). Diện tích của \(D\) được tính theo công thức

	\(S=\displaystyle\int\limits_{a}^{b}\left|f(x)-g(x)\right|\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{b}^{a}\left|f(x)-g(x)\right|\mathrm{\,d}x\)
	\(S=\pi\displaystyle\int\limits_{a}^{b}\left|f(x)-g(x)\right|\mathrm{\,d}x\)
	\(S=\left|\displaystyle\int\limits_{a}^{b}\left[f(x)-g(x)\right]\mathrm{\,d}x\right|\)

Cho hàm số \(y=f(x)\) liên tục trên \([a;b]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) được xác định bởi công thức

	\(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{b}^{a}\left|f(x)\right|\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\)
	\(S=-\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\)

Cho hàm số \(y=f(x)\) liên tục trên \([a;b]\). Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) (\(a<b\)). Diện tích hình phẳng \(D\) được xác định bởi công thức

	\(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\)
	\(S=\pi\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\)

Trong không gian \(Oxyz\), mặt phẳng \((P)\) cắt trục \(Oz\) tại điểm có cao độ bằng \(2\) và song song với mặt phẳng \((Oxy)\). Phương trình mặt phẳng \((P)\) là

	\(z-2=0\)
	\(x-2=0\)
	\(y+z-2=0\)
	\(x-y-2=0\)

Trong không gian \(Oxyz\), cho điểm \(A(4;-3;2)\). Hình chiếu vuông góc của \(A\) lên các trục tọa độ \(Ox,\,Oy,\,Oz\) lần lượt là \(M,\,N,\,P\). Phương trình mặt phẳng \((MNP)\) là

	\(4x-3y+2z-5=0\)
	\(3x-4y+6z-12=0\)
	\(2x-3y+4z-1=0\)
	\(\dfrac{x}{4}-\dfrac{y}{3}+\dfrac{z}{2}+1=0\)

Trong không gian \(Oxyz\), mặt phẳng \((\alpha)\) cắt ba trục tọa độ lần lượt tại các điểm \(M(8;0;0)\), \(N(0;-2;0)\) và \(P(0;0;4)\). Phương trình mặt phẳng \((\alpha)\) là

	\(\dfrac{x}{8}+\dfrac{y}{-2}+\dfrac{z}{4}=0\)
	\(\dfrac{x}{4}+\dfrac{y}{-1}+\dfrac{z}{2}=1\)
	\(x-4y+2z=0\)
	\(x-4y+2z-8=0\)